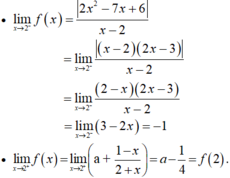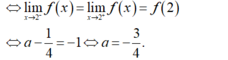Các câu hỏi tương tự
Cho hàm số
f
(
x
)
(
x
+
1
)
2
,
x
1
x
2
+
3
,...
Đọc tiếp
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
Cho hàm số
f
(
x
)
(
x
+
1
)
2
,
x
1
x...
Đọc tiếp
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. K ≢ ± 2
B. K ≢ 2
C. K ≢ - 2
D. K ≢ ± 1
Cho hàm số
f
(
x
)
(
x
+
1
)
2
,...
Đọc tiếp
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Đạo hàm của hàm số \(y=\left(-x^2+3x+7\right)^7\) là:
A. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
B. \(y'=7\left(-x^2+3x+7\right)^6\)
C. \(y'=\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
D. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Đạo hàm của hàm số yleft(x^2-dfrac{2}{x}right)^3là:
A. y6left(x+dfrac{1}{x^2}right)left(x^2-dfrac{2}{x}right)^2
B. y3left(x^2-dfrac{2}{x}right)^2
C. y6left(x-dfrac{1}{x^2}right)left(x^2-dfrac{2}{x}right)^2
D. y6left(x-dfrac{1}{x}right)left(x^2-dfrac{2}{x}right)^2
Đọc tiếp
Đạo hàm của hàm số \(y=\left(x^2-\dfrac{2}{x}\right)^3\)là:
A. \(y'=6\left(x+\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
B. \(y'=3\left(x^2-\dfrac{2}{x}\right)^2\)
C. \(y'=6\left(x-\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
D. \(y'=6\left(x-\dfrac{1}{x}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1. Cho hs yf(x) có đạo hàm thỏa mãn f(6)2. Tính giá trị biểu thức lim _{x-6}dfrac{fleft(xright)-fleft(6right)}{x-6}2. Gọi d là tiếp tuyến của hs ydfrac{x-1}{x+2} tại điểm có hoàng độ bằng -3. Khi đó d tạo với 2 trục tọa độ 1 tam giác có diện tích là bao nhiêu?3. Cho lim _{x-2}dfrac{sqrt{3x+3}-m}{x-2}dfrac{a}{b}với m là số thực và dfrac{a}{b}tối giản. Tính 2a-b4. Cho hàm số yf(x) xác định và có đạo hàm trên tập số thực. Biết f(1)5 và f(1)6. Tìm giới hạn lim _{x-1}dfrac{f^2left(xright)-fleft(xrigh...
Đọc tiếp
1. Cho hs y=f(x) có đạo hàm thỏa mãn f'(6)=2. Tính giá trị biểu thức lim \(_{x->6}\)\(\dfrac{f\left(x\right)-f\left(6\right)}{x-6}\)
2. Gọi d là tiếp tuyến của hs y=\(\dfrac{x-1}{x+2}\) tại điểm có hoàng độ bằng -3. Khi đó d tạo với 2 trục tọa độ 1 tam giác có diện tích là bao nhiêu?
3. Cho lim \(_{x->2}\)\(\dfrac{\sqrt{3x+3}-m}{x-2}\)=\(\dfrac{a}{b}\)với m là số thực và \(\dfrac{a}{b}\)tối giản. Tính 2a-b
4. Cho hàm số y=f(x) xác định và có đạo hàm trên tập số thực. Biết f'(1)=5 và f(1)=6. Tìm giới hạn lim \(_{x->1}\)\(\dfrac{f^2\left(x\right)-f\left(x\right)-30}{\sqrt{x}-1}\)
5. Cho tam giác ABC có 2 trung tuyến kẻ từ A đến B vuông góc với nhau. Khi đó tỉ số \(\dfrac{AC+BC}{AB}\)đạt giá trị lớn nhất bằng bao nhiêu(làm tròn đến hàng phần trăm)
6. Cho tứ diện ABCD có (ACD) vuông góc (BCD), AC=AD=BC=BD=a và CD=2x. Gọi I và J lần lượt là trung điểm của AB và CD. Với giá trị nào của x thì (ABC) vuông góc với (ABD)?
Cho hàm số
f
(
x
)
4
-
x
2
-
2
≤
x
≤...
Đọc tiếp
Cho hàm số f ( x ) = 4 - x 2 - 2 ≤ x ≤ 2 1 x > 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) không xác định tại x = 3
(II) f(x) liên tục tại x = -2
(III) lim x → 2 f ( x ) = 2
A. Chỉ (I).
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Cả (I); (II); (III) đều sai.