Chọn A
ĐKXĐ:
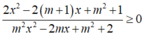
và m2x2 – 2mx+ m2+2≠ 0
+Xét tam thức bậc hai :
f(x) = 2x2 -2( m+1) x+ m2+1
Ta có hệ số a= 2> 0;
∆ = (m+1) 2- 2( m2+1) = -(m-1) 2 ≤ 0
Suy ra với mọi m ta có f(X) ≥ 0 vớ i mọi m(1)
+ Xét tam thức bậc hai:
g(x) = và m2x2 – 2mx+ m2+2
Với m= 0 ta có g(x) = 2> 0
xét với m≠ 0 ta có:
hệ số a= m2> 0
và ∆’ = m2- m2(m2+2) = -m2(m2+1) < 0
Suy ra với mọi m ta có g(x) > 0 với mọi x(2)
Từ (1) và (2) suy ra với mọi m thì
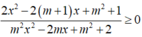
và m2x2 – 2mx+ m2+2≠ 0 đúng với mọi giá trị của x
Vậy tập xác định của hàm số là D = R









