Các câu hỏi tương tự
Cho hàm số
f
(
x
)
|
8
x
4
+
a
x
2
+
b
|
, trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn...
Đọc tiếp
Cho hàm số f ( x ) = | 8 x 4 + a x 2 + b | , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn khẳng định đúng?
A. ![]() ,
, ![]()
B. ![]() ,
, ![]()
C. ![]() ,
, ![]()
D. ![]() ,
, ![]()
Cho hàm số
f
(
x
)
|
8
cos
4
x
+
a
cos
2
x
+
b
|
, trong đó a, b là tham số thực. Gọi M là giá trị lớn nhất của hàm...
Đọc tiếp
Cho hàm số f ( x ) = | 8 cos 4 x + a cos 2 x + b | , trong đó a, b là tham số thực. Gọi M là giá trị lớn nhất của hàm số. Tính tổng a+b khi M nhận giá trị nhỏ nhất.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Xét hàm số f(x) = | x 2 + a x + b |, với a,b là tham số. Gọi M là giá trị lớn nhất của hàm số trên [-1;3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.
A. 2
B. 4
C. -4
D. 3
Xét hàm số
f
(
x
)
|
x
2
+
a
x
+
b
|
, với a, blà tham số. Gọi M là giá trị lớn nhất của hàm số trên [-1;3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a+2b. A.3 B.4 C. -4 D.2
Đọc tiếp
Xét hàm số f ( x ) = | x 2 + a x + b | , với a, blà tham số. Gọi M là giá trị lớn nhất của hàm số trên [-1;3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a+2b.
A.3
B.4
C. -4
D.2
Cho hàm số y f( x) đạo hàm f’ (x) -x2- 1. Với các số thực dương a, b thỏa mãn a b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng A. f(a) B.
f
a
b
C. f( b) D.
f
a
+
b
2
Đọc tiếp
Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
A. f(a)
B. f a b
C. f( b)
D. f a + b 2
Cho hàm số f(x)
x
-
1
2
a
x
2
+
4
a
x
-
a
+
b
-
2
, với a,b
∈
ℝ
. Biết trên khoảng...
Đọc tiếp
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Cho hàm số
f
(
x
)
x
3
+
8
x
+
m...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 8 x + m x - 1 k h i x ≠ 1 n k h i x = 1 , với m,n là các tham số thực. Biết rằng hàm số f(x) liên tục tại x=1 , khi đó tổng giá trị m+n bằng:
A. 4.
B. 1.
C. 0.
D. 2.
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
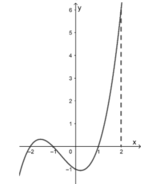
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Cho hàm số
y
f
(
x
)
log
0
,
5
x
-
1
+
m
2
+
m
(m là tham số). Biết rằng có hai giá trị
m
1...
Đọc tiếp
Cho hàm số y = f ( x ) = log 0 , 5 x - 1 + m 2 + m (m là tham số). Biết rằng có hai giá trị m 1 ; m 2 để gía trị nhỏ nhất của hàm số y = f(x) trên đoạn 33 32 ; 1025 1024 bằng 13. Tính T = ( m 1 2 - m 1 ) m 2 2 - m 2
A. T = 9
B. T = 36
C. T = 4
D. T = 64


