Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) 2sin x +m có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng: A. -10 B. -8 C. -6 D. -5
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
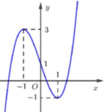
A. -10
B. -8
C. -6
D. -5
Cho hàm số sau: y = f(x) = ( x2 - 2( m + 4) x + 2m + 12).ex. Tìm tổng các giá trị nguyên của m để hàm số nghịch biến trên TXĐ là S thì giá trị của S sẽ là:
A. 15
B. -12
C. -15
D. -10
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Cho hàm số yf(x) có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình
f
(
3
-
4
-
x
2
)
m
có hai nghiệm phân biệt thuộc đoạn
-
2
;
3...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình f ( 3 - 4 - x 2 ) = m có hai nghiệm phân biệt thuộc đoạn - 2 ; 3 . Tìm tập S.
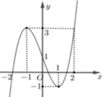
A. S = ( - 1 ; f 3 - 2 ]
B. S = ( f 3 - 2 ; 3 ]
C. S = ○
D. S = [-1;3]
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) m có nghiệm thuộc khoảng
0
;
π
là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số
y
x
-
2
x
-
m
nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số y = x - 2 x - m nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có bảng biến thiên như sauTập hợp tất cả các giá trị của tham số m để phương trình f(x) + m 0 có 2 nghiệm phân biệt là
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như sau
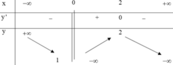
Tập hợp tất cả các giá trị của tham số m để phương trình f(x) + m =0 có 2 nghiệm phân biệt là
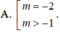
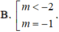
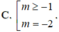
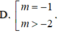
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình
f
(
e
x
)
m
có nghiệm thuộc khoảng (0; ln 3) là: A. (1;3) B.
-
1
3
;
0
C....
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0; ln 3) là:
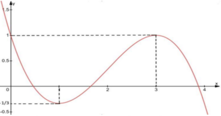
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1






