Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
ln
(
1
+
x
2
+
x
)
. Tập nghiệm của bất phương trình
f
(
a
-
1
)
+
f
(
ln
a
)
≤
0
là:
Đọc tiếp
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số f(x) log2(x - 1). Tìm tập nghiệm của bất phương trình f(x + 1) 1. A. x 2 B. x 4 C. x 1 D. 1 x 2
Đọc tiếp
Cho hàm số f(x) = log2(x - 1). Tìm tập nghiệm của bất phương trình f(x + 1) > 1.
A. x > 2
B. x < 4
C. x > 1
D. 1 < x < 2
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Bảng biến thiên của hàm số yf(x) như hình dưới Tìm m để bất phương trình
m
+
2
sin
x
≤
f
(
x
)
nghiệm đúng với mọi
x
∈
0
;
+
∞
. A. m f(0) +1 B. m f(1) C. m f(0) D. m f(0) -1
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Bảng biến thiên của hàm số y=f'(x) như hình dưới
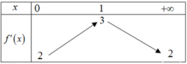
Tìm m để bất phương trình m + 2 sin x ≤ f ( x ) nghiệm đúng với mọi x ∈ 0 ; + ∞ .
A. m < f(0) +1
B. m < f(1)
C. m < f(0)
D. m < f(0) -1
Cho hàm số f(x) log2x và g(x) log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) g(x + 2) A.
S
-
∞
;
1
2
B.
S
-
1
;
1
2
C. S (0; 2). D.
S...
Đọc tiếp
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Cho hàm số f(x)
1
3
x
3
+
x
2
-
3
x
+
1
. Tìm nghiệm của bất phương trình
f
(
x
)
≤
0
Đọc tiếp
Cho hàm số f(x) = 1 3 x 3 + x 2 - 3 x + 1 . Tìm nghiệm của bất phương trình f ' ( x ) ≤ 0
![]()
![]()
![]()
![]()
Cho
f
(
x
)
x
.
e
-
3
x
, tập nghiệm của bất phương trình
f
(
x
)
0
là
Đọc tiếp
Cho f ( x ) = x . e - 3 x , tập nghiệm của bất phương trình f ' ( x ) > 0 là
![]()
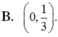
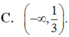
Cho F(x) là một nguyên hàm của hàm số
1
e
x
+
1
, thỏa mãn F(0) –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) 3. A.
S
3
B.
S
-
3
C.
S...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Kí hiệu F(x) là một nguyên hàm của hàm số
f
(
x
)
1
e
x
+
1
, biết F(0) -ln2. Tìm tập nghiệm S của phương trình A. S {-3;3} B. S {3} C.
S
∅
D. S {-3}
Đọc tiếp
Kí hiệu F(x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F(0) = -ln2. Tìm tập nghiệm S của phương trình
A. S = {-3;3}
B. S = {3}
C. S = ∅
D. S = {-3}
cho f(x)=x.e^-3x. tập nghiệm của bất phương trình f'(x)>0 là