Question

Cho hàm số f(x) có đạo hàm liên tục trên [0;1] thỏa mãn điều kiện:

∫ 0 1 f ' x 2 d x = ∫ 0 1 x + 1 e x . f x d x = e 2 - 1 4  và f(1) = 0 Tính giá trị tích phân  I = ∫ 0 1 f x d x

A.  e - 1 2

B. e 2 4

C.  e - 2

D. e 2

Answer 1

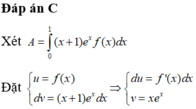
⇒ A = x e x f x 1 0 - ∫ 0 1 x e x f ' x d x = - ∫ 0 1 x e x f ' x d x = 1 - e 2 4

Xét  ∫ 0 1 x 2 e 2 x d x = e 2 x 1 2 x 2 - 1 2 x + 1 4 1 0 = e 2 - 1 4

Ta có  ∫ 0 1 f ' x 2 d x + 2 ∫ 0 1 x e x f ' x d x + ∫ 0 1 x 2 e 2 x f x d x = 0 ⇔ ∫ 0 1 f ' x + x . e x 2 d x = 0 f ' x + x . e x = 0 , ∀ x ∈ 0 ; 1 d o   f ' x + x . e x 2 ≥ 0 ,   ∀ x ∈ 0 ; 1 ⇒ f ' x = - x e x ⇒ f x = 1 - x e x + C f 1 = 0 ⇒ f x = 1 - x e x ⇒ I = ∫ 0 1 f x d x = ∫ 0 1 1 - x e x d x = 2 - x e x 1 0 = e - 2