Đáp án A
Ycbt ⇔ đường thẳng d đi qua điểm uốn của đồ thị C (*)
Ta có:
f ' x = 3 x 2 − 6 x ⇒ f ' ' x = 6 x − 6 = 0 ⇔ x = 1
suy ra điểm uốn I 1 ; − 3
Do đó * ⇔ − 3 = 1 + m ⇔ m = − 4 ∈ − 5 ; − 3
Đáp án A
Ycbt ⇔ đường thẳng d đi qua điểm uốn của đồ thị C (*)
Ta có:
f ' x = 3 x 2 − 6 x ⇒ f ' ' x = 6 x − 6 = 0 ⇔ x = 1
suy ra điểm uốn I 1 ; − 3
Do đó * ⇔ − 3 = 1 + m ⇔ m = − 4 ∈ − 5 ; − 3
Cho hàm số y = x 3 − m x 2 + 3 x + 1 và M 1 ; − 2 . Biết có 2 giá trị của m là m 1 và m 2 để đường thẳng Δ : y = x + 1 cắt đồ thị tại 3 điểm phân biệt A 0 ; 1 , B, C sao cho Δ M B C có diện tích bằng 4 2 . Hỏi m 1 2 + m 2 2 thuộc khoảng nào trong các khoảng nào sau đây
A. 15 ; 17
B. 3 ; 5
C. 31 ; 33
D. 16 ; 18
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
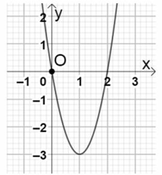
Cho hàm số f x = a x 3 + b x 2 + c x + d có đồ thị (C). Đồ thị hàm số y = f ' x được cho như hình vẽ bên. Biết rằng đường thẳng d : y = x cắt (C) tạo thành hai phần hình phẳng có diện tích bằng nhau. Tổng a + b + c + d bằng
A. 2
B. 3
C. 1
D. 0
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
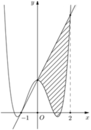
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Biết đường thẳng y=(3m-1)x+6m+3 cắt đồ thị hàm số y = x 3 - 3 x 2 + 1 tại 3 điểm phần biệt sao cho có một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A. (-1;0)
B. (0;1)
C . 1 ; 3 2
D . 3 2 ; 2
Đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3). Mệnh đề nào sau đây là đúng?
A. m ∈ - ∞ ; 0
B. m ∈ 0 ; 2
C. m ∈ 2 ; 4
D. m ∈ 4 ; + ∞
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0