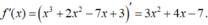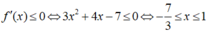Các câu hỏi tương tự
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho hàm số
f
(
x
)
x
3
+
2
x
2
−
7
x
+
3
. Để
f
(
x
)
≤
0
thì x có giá trị thuộc tập hợp nào? A.
−
7
3
;...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 2 x 2 − 7 x + 3 . Để f ' ( x ) ≤ 0 thì x có giá trị thuộc tập hợp nào?
A. − 7 3 ; 1
B. − 1 ; 7 3
C. − 7 3 ; 1
D. − 7 3 ; 1
Cho hàm số
f
(
x
)
2
x
−
3
x
2
. Để
f
(
x
)
0
thì x có giá trị thuộc tập hợp nào dưới đây? A.
−
∞
;
1
3...
Đọc tiếp
Cho hàm số f ( x ) = 2 x − 3 x 2 . Để f ' ( x ) < 0 thì x có giá trị thuộc tập hợp nào dưới đây?
A. − ∞ ; 1 3
B. 0 ; 1 3
C. 1 3 ; 2 3
D. 1 3 ; + ∞
Cho hàm số
f
(
x
)
2
x
-
3
x
2
. Để f(x) 0 thì x có giá trị thuộc tập hợp nào dưới đây? A.
-
∞
;
1
3
B.
0
;
1
3
C. ...
Đọc tiếp
Cho hàm số f ( x ) = 2 x - 3 x 2 . Để f'(x) < 0 thì x có giá trị thuộc tập hợp nào dưới đây?
A. - ∞ ; 1 3
B. 0 ; 1 3
C. 1 3 ; 2 3
D. 1 3 ; + ∞
Câu 1:Cho f(x) dfrac{sqrt{x+2}-sqrt{2-x}}{x}, x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x0?Câu 2:Xét tính liên tục của hàm sốa, f(x) left{{}begin{matrix}x+dfrac{3}{2}dfrac{sqrt{x+1}-1}{sqrt[3]{1+x}-1}end{matrix}right.khi x≤0 và x0 tại xo0b, f(x) left{{}begin{matrix}dfrac{x^3-x^2+2x-2}{x-1}3x+aend{matrix}right.với x1 và với x≥1, xo1
Đọc tiếp
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
cho hàm số y = f(x) = acos(x) -b và y = g(x) = asin(x) +2b -3 và a là số dương. tính a+b sao cho GTLN f(x) =1, GTNN g(x) =3
A. 8
B. 23
C. 15
D.7
GIẢI TỰ LUẬN HỘ MK NHA
Cho hàm số:
f
x
6
-
2
x
+
1
v
ớ
i
x
≤
3...
Đọc tiếp
Cho hàm số: f x = 6 - 2 x + 1 v ớ i x ≤ 3 a x v ớ i x > 3
Với giá trị nào của a thì hàm số f(x) liên tục tại x=3?
A. a=-2
B. a=3
C. a=-1/3
D. a=1/3
Cho hàm số:
f
x
6
-
2
x
+
1
v
ớ
i
x
≤
3...
Đọc tiếp
Cho hàm số: f x = 6 - 2 x + 1 v ớ i x ≤ 3 a x v ớ i x > 3
Với giá trị nào của a thì hàm số f(x) liên tục tại x=3?
A. a=3
B. a=1/3
C. a=-1/3
D. a=-2
Cho hàm số g(x) = x.f(x) + x với f(x) là hàm số có đạo hàm trên R. Biết g'(3) = 2, f'(3) = -1 Giá trị của g(3) bằng:
A. -3
B. 3
C. 20
D. 15