Question

Cho hàm số có đạo hàm f'(x)=x^2(x-1)(x-2)^3 xét các mệnh đề sau đây mệnh đề nào đúng: a.f(-2)<f(-1) b.f(căn2)>f(căn3) c.f(2024)<f(2025) d.f(1/2024)<f(1/2025)

Answer 1

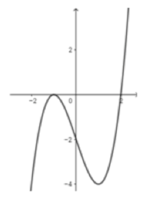
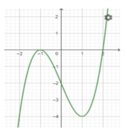
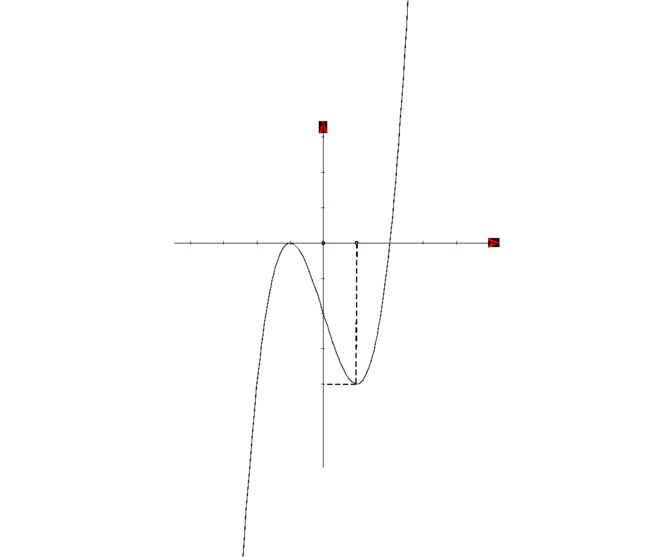
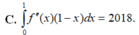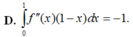\(f'\left(x\right)=0\Rightarrow x=1;2\) (chỉ quan tâm nghiệm bội lẻ, còn x=0 là nghiệm bội chẵn ko cần quan tâm)

BBT:

Từ BBT ta thấy A, B, C đúng

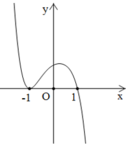
Hàm đồng biến trên \(\left(-\infty;1\right)\)

\(-2;-1\in\left(-\infty;1\right)\) nên \(-2< -1\Leftrightarrow f\left(-2\right)< f\left(-1\right)\)

Do \(\sqrt{2};\sqrt{3}\) cùng thuộc \(\left(1;2\right)\)

Hàm nghịch biến trên \(\left(1;2\right)\) nên \(\sqrt{2}< \sqrt{3}\Leftrightarrow f\left(\sqrt{2}\right)>f\left(\sqrt{3}\right)\)

2024 và 2025 cùng thuộc \(\left(2;+\infty\right)\)

Hàm đồng biến trên \(\left(2;+\infty\right)\) nên \(2024< 2025\Leftrightarrow f\left(2024\right)< f\left(2025\right)\)

Answer 2

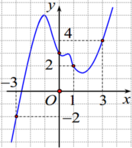
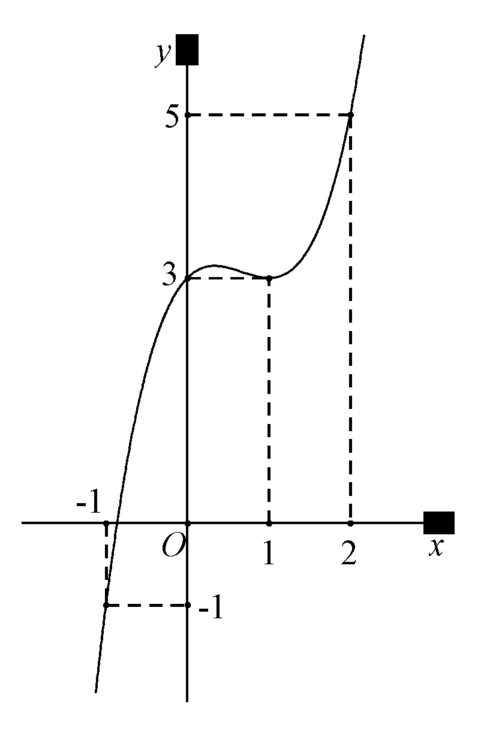
Lập bảng biến thiên tại \(x=0;x=1;x=2\) ta được

Hàm số tăng \(\left(-\infty;1\right)\cup\left(2;+\infty\right)\)

Hàm số giảm \(\left(1;2\right)\)

a) \(f\left(-2\right)< f\left(-1\right):đúng\)

b) \(f\left(\sqrt{2}\right)>f\left(\sqrt{3}\right):Sai\) vì \(\sqrt{2};\sqrt{3}\) thuộc \(\left(1;2\right)\)

c) \(f\left(2024\right)< f\left(2025\right):đúng\)

d) \(f\left(\dfrac{1}{2024}\right)< f\left(\dfrac{1}{2025}\right):đúng\) vì \(\dfrac{1}{2024};\dfrac{1}{2025}\) đều thuộc \(\left(0;1\right)\)