Đáp án B
Đặt z 1 = x 1 + y 1 i và z 2 = x 2 + y 2 i với x 1 , x 2 , y 1 , y 2 ∈ ℝ .
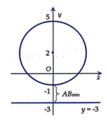
z 1 − 2 i = 3 ⇔ x 1 2 + y 1 − 2 2 = 9 ⇒ tập hợp các số phức z 1 là đường tròn C : x 2 + y − 2 2 = 9 .
z 2 + 2 + 2 i = z 2 + 2 + 4 i
⇔ x 2 + 2 2 + y 2 + 2 2 = x 2 + 2 2 + y 2 + 4 2 ⇔ y 2 + 3 = 0
Þ Tập hợp các số phức z 2 là đường thẳng d : y = − 3 .
Ta có P = z 1 − z 2 = x 2 − x 1 2 + y 2 − y 1 2 đây chính là khoảng cách từ B x 2 ; y 2 ∈ d điểm đến điểm A x 1 ; y 1 ∈ C .
Do đó z 2 − z 1 min ⇔ A B min .
Dựa vào hình vẽ ta tìm được A B min = 2 khi A 0 ; − 1 , B 0 ; − 3 .



