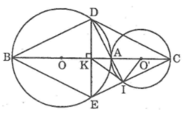
Vì đường tròn (O) và (O’) tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng
Ta có: KB = KC (gt)
Trong đường tròn (O) ta có:
AB ⊥ DE tại K
Suy ra: KD = KE (đường kính vuông góc với dây cung)
Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi.









