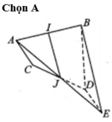
Gọi E là điểm đối xứng của A qua J, suy ra AC = DE.
Khi đó AC+BD = DE+BD > BE hơn nữa BE=2IJ (do IJ là đường trung bình của tam giác ABE)
Vậy AC+BC > 2IJ

Gọi E là điểm đối xứng của A qua J, suy ra AC = DE.
Khi đó AC+BD = DE+BD > BE hơn nữa BE=2IJ (do IJ là đường trung bình của tam giác ABE)
Vậy AC+BC > 2IJ
Cho tứ diện ABCD có A B = C D = 2 3 . Gọi M và N lần lượt là trung điểm các cạnh AC, BD. Biết rằng MN = 3. Số đo góc hợp bởi hai đường thẳng AB, CD bằng
A. 30 °
B. 60 °
C. 90 °
D. 45 °
Cho hình tứ diện ABCD có M,N lần lượt là trung điểm của AB,BD Các điểm G,H lần lượt trên cạnh AC, CD sao cho NH cắt MG tại I Khẳng định nào sau đây là khẳng định đúng?
A. A,C,I thẳng hàng
B. B,C,I thẳng hàng
C. N,G,H thẳng hàng
D. B,G,H thẳng hàng
Cho hình chóp SABCD có đáy ABCD là một tứ giác (AB không song song CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB, O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau
A. SO và AD
B. MN và SC
C. SA và BC
D. MN và SO
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d → . Khẳng định nào sau đây đúng?
A. M P → = 1 2 d → + c → - b →
B. M P → = 1 2 c → + d → + b →
C. M P → = 1 2 c → + b → - d →
D. M P → = 1 2 d → + b → - c →
Cho hình thang ABCD, đáy AB < CD, độ dài hai đường chéo AC và BD lần lượt là m và n, AB + CD = d. Tính diện tích hình thang ABCD theo m,n,d.
1) cho tam giác ABC,có AB< AC ,trên 2 cạnh AB và AC lấy D và E sao cho BD = CE ,gọi M ,N,I lần lượt là trung điểm của BC ,DE ,CD đoạn thẳng MN cắt ABvaAC tại P và Q
a)cm tam giác MIN cân
b)cm tam gia DME cân
c)cm MNsong song với đường phân giác góc A của tam giác ABC
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên BD lấy điểm K sao cho BK = 2KD. Gọi E là giao điểm của JK và CD; F là giao điểm của IE và AD. Tìm giao điểm của AD và (IJK).
A. Điểm I
B. Điểm E
C. Điểm F
D. Điểm K
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp α qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của α với BD và AD. Xét các mệnh đề sau:
(1) MP // BC (2) MQ // AC (3) PQ // AI (4) (MPQ) // (ABC)
Số mệnh đề đúng là:
A. 1
B. 3
C. 2
D. 4