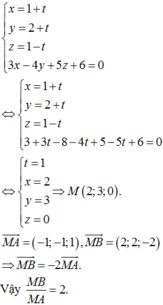Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Trong không gian Oxyz cho hai điểm A(1;2;1) và B(4;5;-2) Đường thẳng AB cắt mặt phẳng (P) :3x – 4y + 5z + 6 0 tại điểm M Tính tỉ số BM/AM A. 2 B. 4 C. 1/4 D. 3
Đọc tiếp
Trong không gian Oxyz cho hai điểm A(1;2;1) và B(4;5;-2) Đường thẳng AB cắt mặt phẳng (P) :3x – 4y + 5z + 6 =0 tại điểm M Tính tỉ số BM/AM
A. 2
B. 4
C. 1/4
D. 3
Trong không gian Oxyz cho điểm A (1;2;-3) và mặt phẳng (P): 2x + 2y - z + 9 0 Đường thẳng d đi qua A vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 1 0 và cắt mặt phẳng (P) tại điểm B. Điểm M nằm trong (P) sao cho M luôn nhìn AB dưới góc vuông. Tính độ dài lớn nhất của MB A.
41
2
B.
5
2
C.
5
D.
41
Đọc tiếp
Trong không gian Oxyz cho điểm A (1;2;-3) và mặt phẳng (P): 2x + 2y - z + 9 = 0 Đường thẳng d đi qua A vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 1 = 0 và cắt mặt phẳng (P) tại điểm B. Điểm M nằm trong (P) sao cho M luôn nhìn AB dưới góc vuông. Tính độ dài lớn nhất của MB
A. 41 2
B. 5 2
C. 5
D. 41
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P): 2x+2y-z+00. Đường thẳng d đi qua A và vuông góc với mặt phẳng (Q): 3x+4y-4z+50 cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) sao cho M luôn nhìn AB dưới góc vuông và độ dài MB lớn nhất. Tính độ dài MB. A.
M
B
41
2
B.
M
B
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P): 2x+2y-z+0=0. Đường thẳng d đi qua A và vuông góc với mặt phẳng (Q): 3x+4y-4z+5=0 cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) sao cho M luôn nhìn AB dưới góc vuông và độ dài MB lớn nhất. Tính độ dài MB.
A. M B = 41 2
B. M B = 5 2
C. M B = 5
D. M B = 41
Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; 2;-3) và mặt phẳng(P):2x+2y-z+90. Đường thẳng d đi qua A và có véctơ chỉ phương
u
⇀
(3;4;-4) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc
90
°
. Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
A
.
H
(
-
2
;
-
1
;
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; 2;-3) và mặt phẳng(P):2x+2y-z+9=0. Đường thẳng d đi qua A và có véctơ chỉ phương u ⇀ =(3;4;-4) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc 90 ° . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
A . H ( - 2 ; - 1 ; 3 )
B . I ( - 1 ; - 2 ; 3 )
C . K ( 3 ; 0 ; 15 )
D . J ( - 3 ; 2 ; 7 )
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng
d
1
:
x
-
1
1
y
+
1
1
z
-
3
-
1
;
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng P : 2 x + 3 y + 4 z - 6 = 0 , cắt đường thẳng d 1 , d 2 lần lượt tại M và N sao cho A M → A N → = 5 và điểm N có hoành độ nguyên.
A. d : x - 2 1 = y - 2 = z - 2 1
B. d : x - 3 1 = y - 1 2 = z - 1 - 2
C. d : x 3 = y + 2 2 = z - 4 - 3
D. d : x - 1 4 = y + 1 - 4 = z - 3 1
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có tâm I(1;-1) và bán kính R=5. Biết rằng đường thẳng ( d ) : 3 x - 4 y + 8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB
A. 8
B. 4
C. 3
D. 6
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
(
1
;
2
;
−
3
)
và mặt phẳng
P
:
2
x
+
2
y
−
z
+
9
0.
Đường thẳng đi qua A và vuông góc với mặt phẳng
Q
:
3
x
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A ( 1 ; 2 ; − 3 ) và mặt phẳng P : 2 x + 2 y − z + 9 = 0. Đường thẳng đi qua A và vuông góc với mặt phẳng Q : 3 x + 4 y − 4 z + 5 = 0 cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) sao cho M luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Độ dài MB là:
A. M B = 5
B. M B = 5 2
C. M B = 41 2
D. M B = 41
Trong không gian Oxyz, cho đường thẳng
∆
:
x
2
y
+
1
-
3
z
+
4
-
3
và mặt phẳng
P
:
2
x
+
y...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng ∆ : x 2 = y + 1 - 3 = z + 4 - 3 và mặt phẳng P : 2 x + y - z - 3 = 0 . Đường thẳng d đi qua M 2 ; - 3 ; - 4 cắt ∆ và (P) lần lượt tại A, B sao cho M là trung điểm của AB có phương trình là
A. x = 2 t y = 2 - 3 t z = 6 - 4 t
B. x = 2 y = - 2 + t z = - 1 + 3 t
C x = 2 + 2 t y = 3 z = - 4 + 6 t
D. x = 2 y = - 3 + 2 t z = - 4 + 3 t
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình
x
-
2
2
+
y
+
2
2
4
và đường thẳng
d
:
3
x
+
4
y
+
7
0
. Gọi A B, là các...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình x - 2 2 + y + 2 2 = 4 và đường thẳng d : 3 x + 4 y + 7 = 0 . Gọi A B, là các giao điểm của đường thẳng d với đường tròn (C) . Tính độ dài dây cung AB.
A. AB = 3 .
B. AB = 2 5 .
C. AB = 2 3 .
D. AB = 4 .