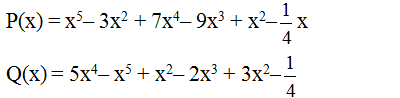Các câu hỏi tương tự
Cho hai đa thức :
P(x)=5x5+3x-4x4-2x3+6+4x2
Q(x)=2x4-x+3x2-2x3+1414 - x5
a/ sắp xếp mỗi hạng tử của đa thức theo lũy thừa giảm của biến .
b/ tính: P(x)+Q(x) ; P(x)-Q(x)
c/ chúng tỏ rằng x= -1 là nghiệm P(x) nhưng không là nghiệm của Q(x)
Giúp mình với Câu 2: Cho hai đa thức: A(x) = –2x3 + 3x + 4x2 + 5x5 +6 –4x4 B(x) = 2x4 – x + 3x2 – 2x3 + 4 – x5. a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm của biến? b) Tính: A(x) + B(x); A(x) – B(x)?
Cho hai đa thức:
P(x)=x5−3x2+7x4−9x3+x2−14x
Q(x)=5x4−x5+x2−2x3+3x2−14
a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
b) Tính P(x) + Q(x) và P(x) - Q(x).
c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x).
dễ ợt!! nhanh mk tk cho
Cho các đa thức : P(x) = x5 - 3x2 + 7x4 - 9x3 + x2 - \(\dfrac{1}{4}\)x ; Q(x) = 5x4 - x5 + x2 - 2x3 + 3x2 - \(\dfrac{1}{4}\)
a ) sắp xếp hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến
b ) Tính P(x) + Q(x)
Bài 1. Cho hai đa thức:P(x) 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6xQ(x) x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảmdần của biến.b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).Bài 2. Cho hai đa thức:P(x) x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3Q(x) (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảmdần của biến.b) Tính P(x) + Q(x), P(x) - Q(x)Bài 5. Cho hai đa thức:...
Đọc tiếp
Bài 1. Cho hai đa thức:
P(x) = 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6x
Q(x) = x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).
Bài 2. Cho hai đa thức:
P(x) = x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3
Q(x) = (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính P(x) + Q(x), P(x) - Q(x)
Bài 5. Cho hai đa thức:
P(x) = 2x4 + 2x3 - 3x2 + x +6
Q(x) = x4 - x3 - x2 + 2x + 1
a) Tính P(x) + Q(x), P(x) - Q(x)
b) Tính và P(x) - 2Q(x).
Bài 6. Cho đa thức P(x) = 2x4 - x2 +x - 2.
Tìm các đa thức Q(x), H(x), R(x) sao cho:
a) Q(x) + P(x) = 3x4 + x3 + 2x2 + x + 1
b) P(x) - H(x) = x4 - x3 + x2 - 2
c) R(x) - P(x) = 2x3 + x2 + 1
: Cho hai đa thức:
a) Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
b) Tính P(x) + Q(x) và P(x) – Q(x).
c) Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x).
cho các đa thức
P[x]= 3x^5 + 5x - 4x^4 - 2x^3 + 6 + 4x^2
Q[x]= 2x^4 -x + 3x^2 - 2x^3 + 1/4 - x^5
a, sắp xếp các hạng tử của đa thức theo lũy thừa giảm của biến
b, tính P[x] + Q[x] ; P[x] - Q[x]
c, chứng tỏ rằng x= -1 là nghiệm của P[x] nhưng không phải là nghiệm của Q[x]
thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến P(x)=4x5-3x2+3x-2x3-4x5+x4-5x+1+4x2 Q(x)=x7-2x6+2x3-2x4-x7+x5+2x6-x+5+2x4-x5 b)tính p(x)+Q(x);P(x)-Q(x)
Cho 2 đa thức : P(x)=x³-2x⁴+x²-5+5x Q(x)=x⁴+4x²-3x³-6x+7 a)sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm của biến b)tính P(x)+Q(x) c)tính P(x)-Q(x) d)chứng tỏ rằng x=1 là nghiệm của P(x)nhưng ko là nghiệm của Q(x)