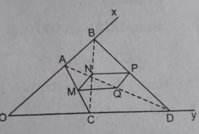
Vì MNPQ là hình chữ nhật nên ∠ (xOy) = 1v.

Vì MNPQ là hình chữ nhật nên ∠ (xOy) = 1v.
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.
Tìm điều kiện của góc xOy và các đoạn thẳng AB, CD để tứ giác MNPQ là: Hình vuông
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.
Tìm điều kiện của góc xOy và các đoạn thẳng AB, CD để tứ giác MNPQ là: Hình thoi
Cho goc xOy khác góc bẹt . Trên tia Ox lấy 2 điểm A và B (A nằm giữa O và B), trên tia Oy lấy 2 điểm C và D (C nằm giữa O và D) .Gọi MNPQ theo thứ tự trung điểm của AC,BC,BD và AD. tìm điều kiện của góc xOy và các đoạn thẳng AB , CD để tứ giác MNPQ là:
a) Hình chữ nhật
b) hình thoi
c) Hình vuông
Trên hai cạnh Ox và Oy của góc nhọn xOy đặt các đoạn thẳng AB và CD sao cho AB=CD. Điểm A nằm giữa O và B , Điểm C nằm giữa O và D , OA khác OC . Gọi E và F lần lượt là trung điểm của AC và BD . M là điểm đối xứng của D qua E
a, chứng minh tam giác ECD = tam giác EAM ?
b, chứng minh EF song song với Ot và Ot là tia phân giác của góc xOy ?
Cho góc xOy khác góc bẹt. Trên tia Õ lấy điểm A và D ( A nằm giữa O và D ) trên tia Oy lấy điểm B và C ( B nằm giữa tia Oy lấy điểm B và C ( B nằm giữa O và C ) sao cho OA = OB ; góc OAC = góc OAB, AC cắt BD tại I. Chứng minh IC = ID
Cho điểm M nằm trong góc xOy nhọn (góc xOy, M cố định). Dựng tia Oz sao cho MOz=xOy (tia Ox nằm giữa hai tia Oy và Oz), lấy điểm N sao cho OM=ON. Gọi T là trung điểm OM và Q thuộc cạnh MN sao cho MQ=3NQ. Đường thẳng TQ cắt tia Oz tại C.
a. Chứng minh rằng: OC=3CN
b. Hai điểm A và B lần lượt di động trên các tia Ox và Oy sao cho 2OA = 3OB (A,B khác O). Xác định vị trí điểm A sao cho 2MA+3MB nhỏ nhất.
Cho góc xOy, trên tia Ox lấy điểm M, N (M nằm giữa O và N), Trên tia Oy lấy điểm P,Q( P nằm giữa O và Q) sao cho góc ONP = góc OQM. a) Chứng minh ∆ONP đồng dạng với ∆OQM b) Chứng minh OM.ON = OP.OQ c) Gọi I là giao điểm của PN và MQ. Chứng minh IM.IQ = IN.IP
1. Trên hai cạnh của góc nhọn xOy, đặt các đoạn thẳng AB và CD bằng nhau (A giữa O và B, C nằm giữa O và D). I và E lần lượt là trung điểm của AC và BD. Chứng minh rằng đường thẳng IE song song với tia phân giác của góc xOy.
Giúp mình với nha!!!
2. Cho hình chữ nhật ABCD. Ta nối đỉnh A với một điểm E bất kỳ trên đường chéo DB rồi kéo dài và lấy trên đó một điểm F sao cho
FE = AE . Từ E dựng đường song song với đường chéo AC, đường này cắt BC tại I, và cắt DC kéo dài tại K.
a) Chứng minh: CF // DB
b) Chứng minh: tứ giác FICK là hình chữ nhật.
Cho hình vuông ABCD. Các điểm M, N lần lượt là trung điểm của AB và BC. Gọi O là giao điểm hai đường chéo của hình vuông ABCD; trên đoạn thẳng CN lấy điểm E sao cho E nằm giữa C và N. Vẽ tia Ox nằm giữa hai tia OD và OC sao cho góc EOx = 45 độ, tia Ox cắt DC tại F. Chứng minh rằng: góc AFD = góc BME.