MNPQ là hình vuông ⇔ ∠ (xOy) = 1v và AB = CD.

MNPQ là hình vuông ⇔ ∠ (xOy) = 1v và AB = CD.
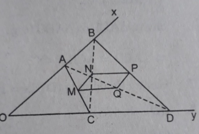
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.
Tìm điều kiện của góc xOy và các đoạn thẳng AB, CD để tứ giác MNPQ là: Hình chữ nhật
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.
Tìm điều kiện của góc xOy và các đoạn thẳng AB, CD để tứ giác MNPQ là: Hình thoi
Cho goc xOy khác góc bẹt . Trên tia Ox lấy 2 điểm A và B (A nằm giữa O và B), trên tia Oy lấy 2 điểm C và D (C nằm giữa O và D) .Gọi MNPQ theo thứ tự trung điểm của AC,BC,BD và AD. tìm điều kiện của góc xOy và các đoạn thẳng AB , CD để tứ giác MNPQ là:
a) Hình chữ nhật
b) hình thoi
c) Hình vuông
Trên hai cạnh Ox và Oy của góc nhọn xOy đặt các đoạn thẳng AB và CD sao cho AB=CD. Điểm A nằm giữa O và B , Điểm C nằm giữa O và D , OA khác OC . Gọi E và F lần lượt là trung điểm của AC và BD . M là điểm đối xứng của D qua E
a, chứng minh tam giác ECD = tam giác EAM ?
b, chứng minh EF song song với Ot và Ot là tia phân giác của góc xOy ?
Cho góc xOy khác góc bẹt. Trên tia Õ lấy điểm A và D ( A nằm giữa O và D ) trên tia Oy lấy điểm B và C ( B nằm giữa tia Oy lấy điểm B và C ( B nằm giữa O và C ) sao cho OA = OB ; góc OAC = góc OAB, AC cắt BD tại I. Chứng minh IC = ID
Cho hình vuông ABCD. Các điểm M, N lần lượt là trung điểm của AB và BC. Gọi O là giao điểm hai đường chéo của hình vuông ABCD; trên đoạn thẳng CN lấy điểm E sao cho E nằm giữa C và N. Vẽ tia Ox nằm giữa hai tia OD và OC sao cho góc EOx = 45 độ, tia Ox cắt DC tại F. Chứng minh rằng: góc AFD = góc BME.
Cho điểm M nằm trong góc xOy nhọn (góc xOy, M cố định). Dựng tia Oz sao cho MOz=xOy (tia Ox nằm giữa hai tia Oy và Oz), lấy điểm N sao cho OM=ON. Gọi T là trung điểm OM và Q thuộc cạnh MN sao cho MQ=3NQ. Đường thẳng TQ cắt tia Oz tại C.
a. Chứng minh rằng: OC=3CN
b. Hai điểm A và B lần lượt di động trên các tia Ox và Oy sao cho 2OA = 3OB (A,B khác O). Xác định vị trí điểm A sao cho 2MA+3MB nhỏ nhất.
Cho góc xOy, trên tia Ox lấy điểm M, N (M nằm giữa O và N), Trên tia Oy lấy điểm P,Q( P nằm giữa O và Q) sao cho góc ONP = góc OQM. a) Chứng minh ∆ONP đồng dạng với ∆OQM b) Chứng minh OM.ON = OP.OQ c) Gọi I là giao điểm của PN và MQ. Chứng minh IM.IQ = IN.IP
Cho góc xOy < 90 độ. Trên tia phân giác của góc x Cho góc xOy < 90 độ. Trên tia phân giác của góc xOy lấy điểm A. Qua A, kẻ đường thẳng vuông góc với Ox tại B và đường thẳng vuông góc với Oy tại C.
a) Chứng minh OB = OC.
b)Chứng minh OA là đường trung trực của đoạn thẳng BC.
c) Gọi D là giao điểm của đường thẳng AB với tia Oy, gọi E là giao điểm của đường thẳng AC với tia Ox. Chứng minh rằng: tam giác DOE cân.
d) Chứng minh tứ giác BCDE là hình thang.
Giúp mình với, huhuhuhuhu TvT