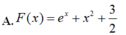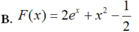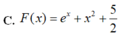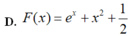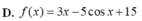\(u=e^x\Rightarrow du=e^xdx\Rightarrow dx=\dfrac{du}{e^x}\)
\(\Rightarrow\int f\left(x\right)dx=\int\dfrac{du}{2u^2+3u}\)
\(\dfrac{1}{2u^2+3u}=\dfrac{A}{u}-\dfrac{B}{2u+3}=\dfrac{A\left(2u+3\right)-Bu}{2u^2+3u}=\dfrac{\left(2A-B\right)u+3A}{2u^2+3u}\)
\(\Rightarrow\left(2A-B\right)u+3A=1\Rightarrow\left\{{}\begin{matrix}2A-B=0\\3A=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=\dfrac{1}{3}\\B=\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\int\dfrac{du}{2u^2+3u}=\dfrac{1}{3}\int\left(\dfrac{1}{u}-\dfrac{2}{2u+3}\right)du=\dfrac{1}{3}\left[lnu-ln\left(2u+3\right)\right]+C\)
\(\Rightarrow F\left(x\right)=\dfrac{1}{3}\left[ln\left(e^x\right)-ln\left(2e^x+3\right)\right]+C=\dfrac{1}{3}\left[x-ln\left(2e^x+3\right)\right]+C\)
\(F\left(0\right)=10\Rightarrow\dfrac{1}{3}\left[x-ln\left(2e^x+3\right)\right]+C=10\Rightarrow C=\dfrac{ln5}{3}+10\)
\(\Rightarrow F\left(x\right)=\dfrac{1}{3}\left[x-ln\left(2e^x+3\right)\right]+\dfrac{ln5}{3}+10\)