Đáp án C
F x = − 1 3 x 3 là một nguyên hàm của f x x nên
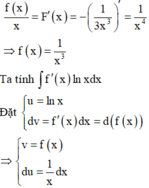
Áp dụng công thức nguyên hàm từng phần ta có
∫ f ' x lnxdx = ∫ lnxd f x = lnx . f x − ∫ f x x dx = lnx x 3 + 1 3 x 3 + C
Đáp án C
F x = − 1 3 x 3 là một nguyên hàm của f x x nên
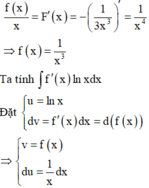
Áp dụng công thức nguyên hàm từng phần ta có
∫ f ' x lnxdx = ∫ lnxd f x = lnx . f x − ∫ f x x dx = lnx x 3 + 1 3 x 3 + C
Cho F ( x ) = 1 2 x 2 là một nguyên hàm của hàm số f ( x ) x . Tính I = ∫ 1 e f ' ( x ) ln x d x :
A. I = 3 − e 2 2 e 2
B. I = e 2 − 3 2 e 2
C. I = 2 − e 2 e 2
D. I = e 2 − 2 e 2
Cho F(x) = a x (lnx+b) là một nguyên hàm của hàm số f ( x ) = 1 + ln x x 2 trong đó a,b ∈ Z. Tính S = a+b
A. S = -2
B. S = 1
C. S = 2
D. S = 0
Họ nguyên hàm F(x) của hàm số f ( x ) = x lnx là
A. F ( x ) = x 2 2 lnx - x 2 2 + C
B. F ( x ) = x 2 2 lnx - x 2 4 + C
C. F ( x ) = x 2 2 lnx + x 2 2 + C
D. F ( x ) = x 2 2 lnx + x 2 4 + C
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F(e)=5. Tính ∫ 1 e ln x . f ( x ) d x
A. I=3
B. I=-3
C. I=2
D. I=-2
Họ nguyên hàm của hàm số f(x)=4x(1+lnx) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Họ các nguyên hàm của hàm số f(x)=(2x+1)lnx là
A. x 2 + x ln x - x 2 2 + x + C
B. x 2 + x ln x - x 2 2 - x + C
C. x 2 + 1 ln x - x 2 2 - x + C
D. 2 ln x + 1 2 + C
Cho hàm số f x = 2 m x + ln x . Tìm m để nguyên âm F(x) của f(x) thỏa mãn F 1 = 0 và F 2 = 2 + 2 ln 2
A. m = 1 2
B. m = 2
C. m = 0
D. m = 1
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Giả sử F(x) là một nguyên hàm của f x = ln x + 3 x 2 sao cho F - 2 + F 1 = 0 . Giá trị của F - 1 + F 2 bằng
A. 10 3 ln 2 - 5 6 ln 5
B. 0
C. 7 3 ln 2
D. 2 3 ln 2 + 3 6 ln 5