Cho em hỏi:
Cho △ABC cân tại A, có AH là đường trung tuyến.
a) Chứng minh: △AHB = △AHC.
b) Tính BC biết AH = 4cm, AB = 5cm.
c) Từ H vẽ HK // AC ( K thuộc AB). Chứng minh △AKH cân và K là trung điểm của AB.
*Lưu ý giúp em:
-Em học lớp 7, khi anh / chị làm bài nhớ vẽ hình vì em không biết hình em đúng không ạ. Câu a giải theo cách tam giác vuông. Xin cảm ơn!
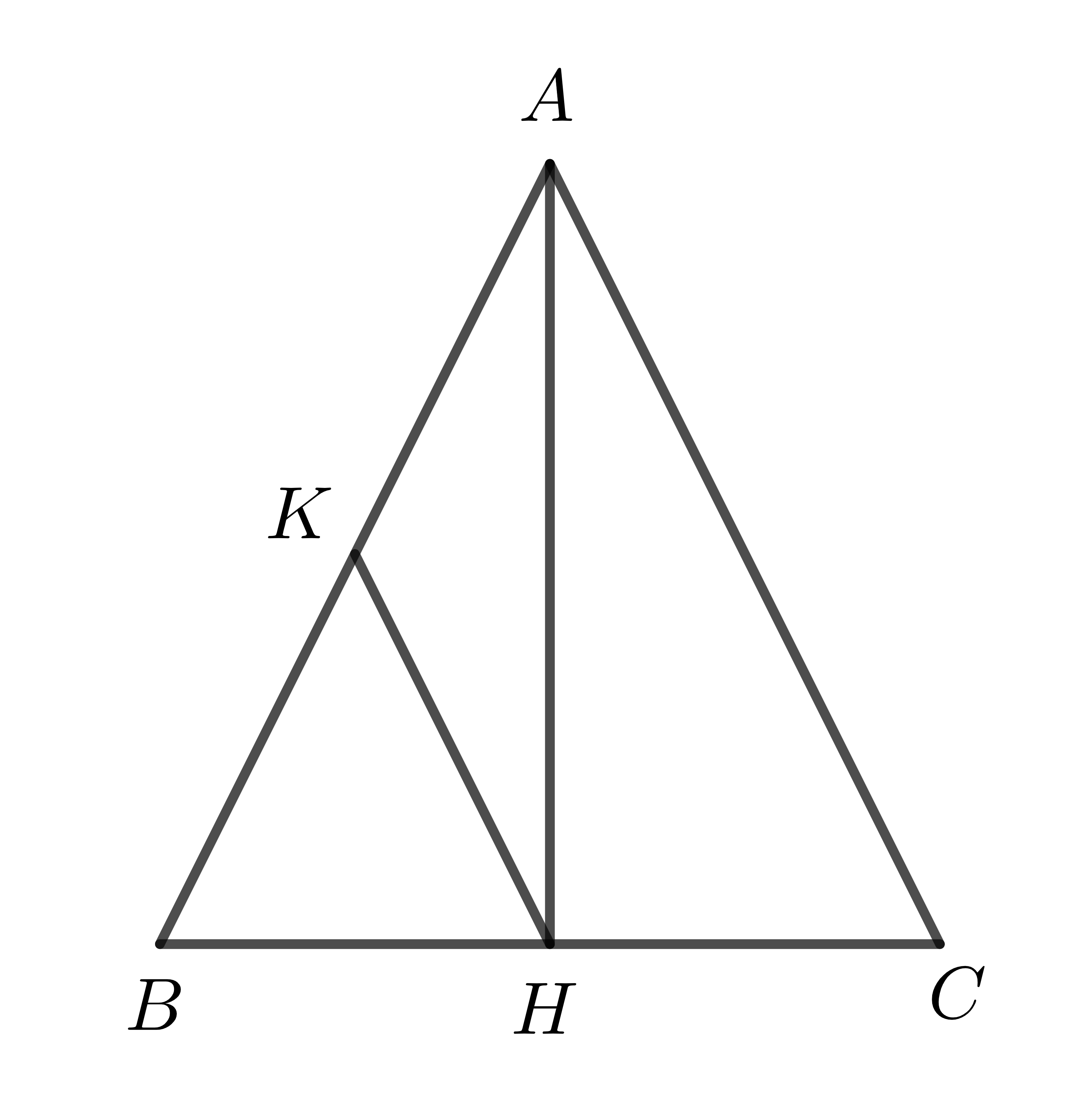
a) Xét \(\Delta ABH\) và \(\Delta ACH\) có
\(AH\) chung
\(AB=AC\) (do \(\Delta ABC\) cân)
\(BH=CH\) (Do \(AH\) là trung tuyến)
\(\Rightarrow\Delta ABH=\Delta ACH\) (c.c.c)
b) Áp dụng định lí Pytago ta có:
\(AB^2=AH^2+BH^2\Rightarrow BH^2=AB^2-AH^2=5^2-4^2=9\)
\(\Rightarrow BH=3\left(cm\right)\Rightarrow BC=2BH=6\left(cm\right)\)
c) Do \(\Delta ABH=\Delta ACH\) nên \(\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)
Lại có \(HK\)// \(AC\) nên \(\widehat{CAH}=\widehat{AHK}\) (so le trong)
\(\Rightarrow\widehat{BAH}=\widehat{AHK}\). Do đó \(\Delta AHK\) cân tại \(K\)
\(\Rightarrow AK=HK\)
Mặt khác \(HK\)// \(AC\) \(\Rightarrow\widehat{BHK}=\widehat{BCA}\) (hai góc đồng vị)
mà \(\widehat{BCA}=\widehat{ABC}\) nên \(\widehat{BHK}=\widehat{ABC}\Rightarrow\Delta BHK\) cân
\(\Rightarrow BK=HK\)
Vậy \(AK=BK\left(=HK\right)\) nên \(K\) là trung điểm \(AB\)













