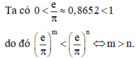Tuyển Cộng tác viên Hoc24 nhiệm kì 28 tại đây: https://forms.gle/GrfwFgzveoKLVv3p6
Các câu hỏi tương tự
Cho hàm số
y
x
3
-
3
x
+
2
C
. Biết rằng đường thẳng
d
:
y
a
x
+
b
cắt đồ thị
C
tại ba điểm phân biệt M, N, P. Tiếp tuyến tại ba điểm M, N, P của đồ thị
C
cắt
C
tại các điểm
M
,...
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 C . Biết rằng đường thẳng d : y = a x + b cắt đồ thị C tại ba điểm phân biệt M, N, P. Tiếp tuyến tại ba điểm M, N, P của đồ thị C cắt C tại các điểm M ' , N ' , P ' (tương ứng khác M, N, P). Khi đó đường thẳng đi qua ba điểm M ' , N ' , P ' có phương trình là
A. y = 4 a + 9 x + 18 - 8 b
B. y = 4 a + 9 x + 14 - 8 b
C. y = a x + b
D. y = - 8 a + 18 x + 18 - 8 b
Cho
a
→
m
i
→
+
(
2
n
-
1
)
j
→
,
b
→
-
n
;
1
+
m...
Đọc tiếp
Cho a → = m i → + ( 2 n - 1 ) j → , b → = - n ; 1 + m Khi đó cặp số (m;n) để a → = b → là
![]()
![]()
![]()
![]()
Cho hình hộp ABCD.A’B’C’D’ có A(1;0;0), B(2;-1;1), D(0;1;1) và A’(1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thànhbởi sáu điểm M, N, P, Q, E, F. A. V
1
3
B. V
1
2
C. V
2
3
D. V
1
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có A(1;0;0), B(2;-1;1), D(0;1;1) và A’(1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thànhbởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
hãy so sánh a phần b với a+m phần b+m (a,b,m e N)
Cho hàm số
f
(
x
)
1
+
c
o
s
x
(
x
-
π
)...
Đọc tiếp
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Cho đồ thị yf’(x) trên [m;n] (như hình vẽ). Biết f(a) f(c)0; f(d)f(b)0 và
m
a
x
f
(
x
)
[
m
;
n
]
f
(
n
)
;
m
i
n...
Đọc tiếp
Cho đồ thị y=f’(x) trên [m;n] (như hình vẽ). Biết f(a)> f(c)>0; f(d)<f(b)<0 và
m
a
x
f
(
x
)
[
m
;
n
]
=
f
(
n
)
;
m
i
n
f
(
x
)
[
m
;
n
]
=
f
(
m
)
Số điểm cực trị của hàm số
y
=
f
(
x
)
trên [m;n] là
A. 6
B. 8
C. 9
D. 10
Cho tam giác ABC. Gọi M là trung điểm của AC, N là trung điểm của AB. Trên tia đối MB lấy điểm E sao cho MB=ME. Trên tia đối NC lấy điểm D sao cho DN= CN.
C/m: D, A, E thẳng hàng
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm
A
a
;
1
. Biết
a
m
n
(với mọi
m
,
n
∈
N
và
m...
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A a ; 1 . Biết a = m n (với mọi m , n ∈ N và m n tối giản) là giá trị để có đúng một tiếp tuyến của (C) đi qua A. Khi đó giá trị m + n là:
A. 2
B. 7.
C. 5
D. 3.
Cho a, b, c 1. Biết rằng biểu thức
P
log
a
b
c
+
log
b
a
c
+
4
log
c
a
b
đạt giá trị nhỏ nhất bằng m khi
log
b
c
n
.
...
Đọc tiếp
Cho a, b, c > 1. Biết rằng biểu thức P = log a b c + log b a c + 4 log c a b đạt giá trị nhỏ nhất bằng m khi log b c = n . Tính giá trị m + n.
A. m + n = 14
B. m + n = 25 2
C. m + n = 12
D. m + n = 10
Cho a,b,c1 Biết rằng biểu thức
P
log
a
b
c
+
log
b
a
c
+
4
log
c
a
b
đạt giá trị nhỏ nhất bằng m khi
log
b
c
n
.
Tính g...
Đọc tiếp
Cho a,b,c>1 Biết rằng biểu thức P = log a b c + log b a c + 4 log c a b đạt giá trị nhỏ nhất bằng m khi log b c = n . Tính giá trị m + n .
A. 12
B. 25/2
C. 14
D. 10