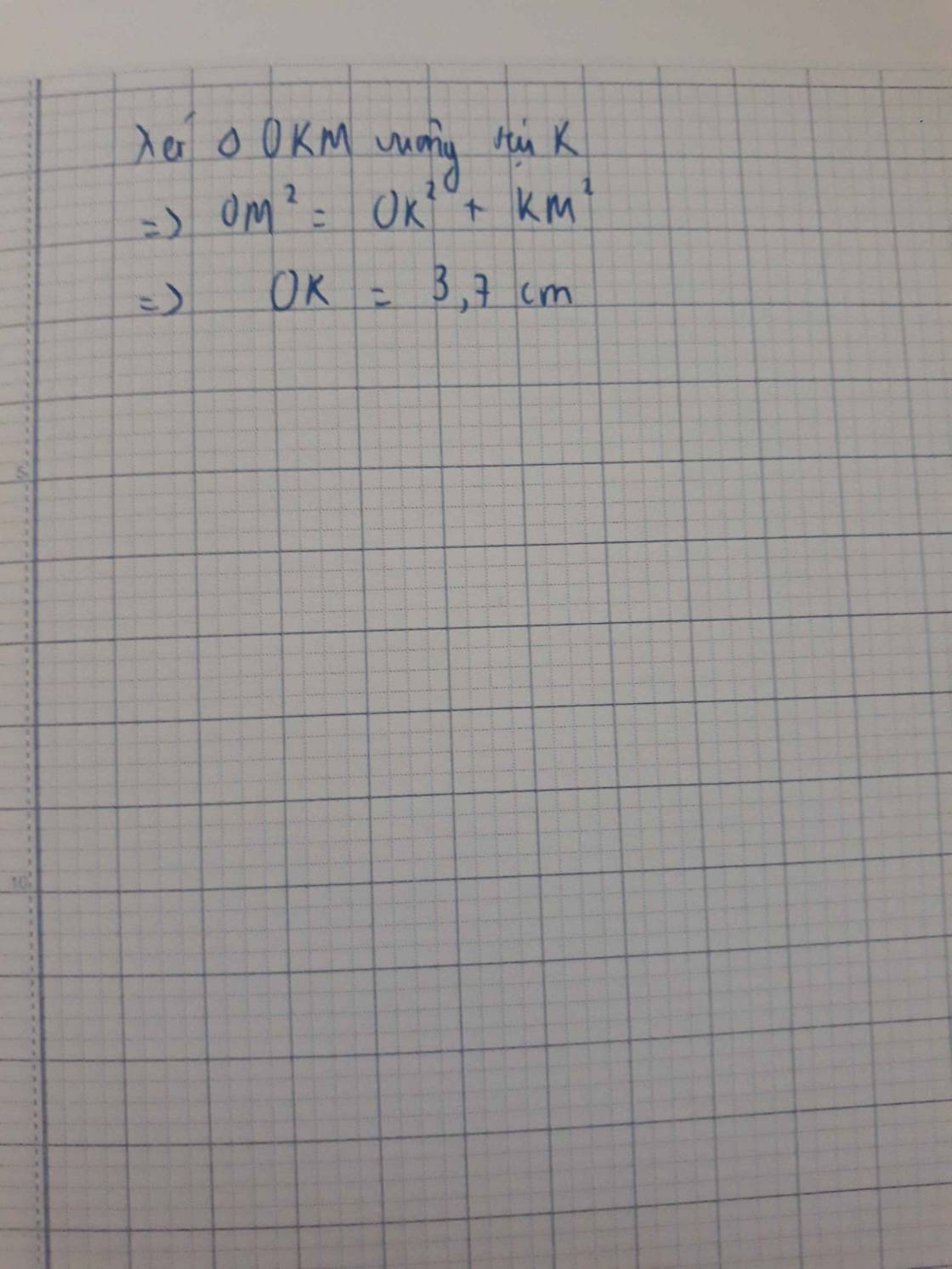Các câu hỏi tương tự
Cho đường tròn tâm O , dây AB = 12 cm. Đường kính MN vuông góc AB tại H. ( \(MH\ge HN\))
a) Chứng minh \(MN\ge6\)
b) MB = 10 tính đường kính đường tròn
Cho đường tròn tâm O bán kính R, dây AB không qua tâm O, I là trung điểm của AB. AB dài 16cm, bán kính R= 10 cm
a) Tính OI
b) OI cắt đường tròn O tại M . Tính AM
c) Kẻ đường kính MN của đường tròn tâm O, kẻ OK vuông góc với AN tại K. Tính AK
Cho nửa đường tròn tâm O đường kính AB = 2R . Điểm C cố định trên nửa đường tròn . Điểm M thuộc cung AC . Kẻ MH vuông góc với AB . Mb cắt CA tại E . Kẻ EI vuông góc với AB . Gọi K là giao điểm của AC và MH . CMR
a , tứ giác BHKC nội tiếp .
b , AK.AC = AM.AM , IE là phân giác của góc MIC
c , AE.AC + BE.BM không phụ thuộc vị trí điểm M
Cho đường tròn (o) bán kính R=12cm dây AB khác đường kính. qua O kẻ đường thẳng vuông góc vs AB cắt tiếp tuyến A của (O) tại M và cắt AB tại H a) Cho OM=15cm . Tính AM, AH và sin AOM b) chứng minh MB là tiếp tuyến của đường tròn
cho nửa đường tròn (o,r) đường kính ab. gọi c là điểm chính giữa cung ab. điểm m thuộc cung ac. hạ mh vuông góc với ab tại h , ac cắt mh tại k, mb cát ac tại e . hạ ei vuông góc với ab tại i
Cho đường trong tâm O bán kính R đường kính AB. Lấy điểm H thuộc OB, dây MN vuông góc với AB tại điểm H. Hạ HE vuông góc với MA, HF vuông góc với MB. Tiếp tuyến của đường tròn tại M cắt AB tại K , đường thẳng EF vắt AB tại I.A/ Chứng minh : I là trung điểm của HKB/ Lấy điểm Q đối xứng với M qua A. Chứng minh : Khi điểm H chuyển động trên đoạn OB thì Q thuộc 1 đường tròn cố định.
Đọc tiếp
Cho đường trong tâm O bán kính R đường kính AB. Lấy điểm H thuộc OB, dây MN vuông góc với AB tại điểm H. Hạ HE vuông góc với MA, HF vuông góc với MB. Tiếp tuyến của đường tròn tại M cắt AB tại K , đường thẳng EF vắt AB tại I.
A/ Chứng minh : I là trung điểm của HK
B/ Lấy điểm Q đối xứng với M qua A. Chứng minh : Khi điểm H chuyển động trên đoạn OB thì Q thuộc 1 đường tròn cố định.
Bài 7: Cho nửa đường tròn (O) đường kính AB2R. Điểm C cố định trên nửa đường tròn. Điểm M thuộc cung AC (M khác A,C). Hạ MH vuông góc AB tại H. Nối MB cắt CA tại E. Hạ EI vuông góc AB tại I. Gọi K là giao điểm của AC và MH. a) Chứng minh: BHKC, AMEI là các tứ giác nội tiếp. b) Chứng minh: AK.AC AM2. c) Chứng minh: AE.AC + BE.BM không phụ thuộc vào vị trí của điểm M. d) Chứng minh: điểm E cách đều 3 cạnh của tam giác MIC. e) Khi M chuyển động trên cung AC thì đường tròn ngoại tiếp tam giác IMC...
Đọc tiếp
Bài 7: Cho nửa đường tròn (O) đường kính AB=2R. Điểm C cố định trên nửa đường tròn. Điểm M thuộc cung AC (M khác A,C). Hạ MH vuông góc AB tại H. Nối MB cắt CA tại E. Hạ EI vuông góc AB tại I. Gọi K là giao điểm của AC và MH. a) Chứng minh: BHKC, AMEI là các tứ giác nội tiếp. b) Chứng minh: AK.AC =AM2. c) Chứng minh: AE.AC + BE.BM không phụ thuộc vào vị trí của điểm M. d) Chứng minh: điểm E cách đều 3 cạnh của tam giác MIC. e) Khi M chuyển động trên cung AC thì đường tròn ngoại tiếp tam giác IMC đi qua hai điểm cố định.
Cho tam giác MAB vuông tại M,MBMA,kẻ MH vuông góc với AB (H thuộc AB).Đường tròn (O) đường kính MH cắt MA,MB lần lượt tại E và F (E,F khác M)a) đường thẳng EF cắt đường tròn (O) ngoại tiếp tam giác MAB tại P và Q (P thuộc cung MB). Chứng minh tam giác MPQ cânb)Gọi I là giao điểm thứ 2 của đường tròn (O) với (O) .Đường thẳng EF cắt đường thẳng AB tại K .Chứng minh M,I,K thẳng hàng
Đọc tiếp
Cho tam giác MAB vuông tại M,MB<MA,kẻ MH vuông góc với AB (H thuộc AB).Đường tròn (O) đường kính MH cắt MA,MB lần lượt tại E và F (E,F khác M)
a) đường thẳng EF cắt đường tròn (O') ngoại tiếp tam giác MAB tại P và Q (P thuộc cung MB). Chứng minh tam giác MPQ cân
b)Gọi I là giao điểm thứ 2 của đường tròn (O) với (O') .Đường thẳng EF cắt đường thẳng AB tại K .Chứng minh M,I,K thẳng hàng
Cho đường tròn tâm O đường kính AD , dây cung AB . QUa B kẻ dây BC vuông góc với AD . Tính bán kính của đường tròn biết AB=10cm , BC=12cm
cho đường tròn tâm o đường kính AB, dây cung CD cắt AB tại M . Biết MC=4cm,MB=12cm,góc MBD=30 độ
Tính khoảng cách từ o đến CD