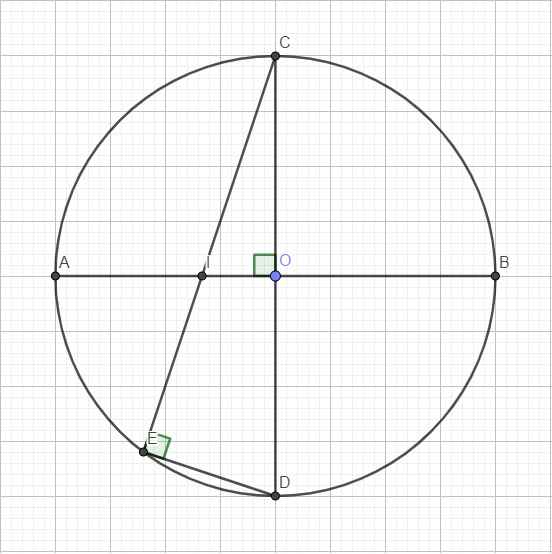
b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
a: Xét (O) có
ΔCED nội tiếp đường tròn
CD là đường kính
Do đó: ΔCED vuông tại E
Xét ΔCOI vuông tại O và ΔCED vuông tại E có
\(\widehat{ICO}\) chung
Do đó: ΔCOI\(\sim\)ΔCED