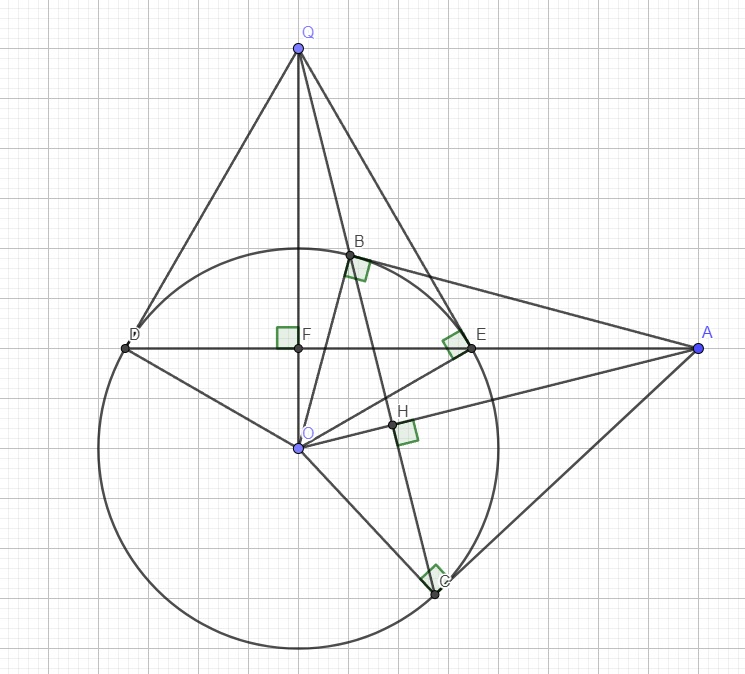
cho đường tròn (O,R) và một điểm A nằm ngoài đường tròn (O). Vẽ tiếp thuyến AB của đường tròn (O)(B là tiếp điểm). Vẽ dây cung BC của (O) vuông góc với OA tại H
a) cm: H là trung điểm của BC
b) cm: AC là tiếp tuyến của (O)
c) với OA=2R. cm : tam giác ABC đều
d) trên tia đối của BC lấy điểm Q bất kì. Vẽ tiếp tuyến QD, QE của (O). cm ba điểm A,D,E thẳng hàng
a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC và OH là phân giác của góc BOC
b: Ta có: OH là phân giác của góc BOC
=>\(\widehat{BOH}=\widehat{COH}\)
=>\(\widehat{BOA}=\widehat{COA}\)
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
mà \(\widehat{OBA}=90^0\)
nên \(\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: ΔOBA=ΔOCA
=>\(\widehat{BAO}=\widehat{CAO}\)
mà tia AO nằm giữa hai tia AB và AC
nên \(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Ta có: ΔOBA=ΔOCA
=>AB=AC
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều
d.
\(\left\{{}\begin{matrix}OD=OE=R\\QD=QE\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OQ\) là trung trực DE \(\Rightarrow OQ\perp DE\) , gọi giao điểm của chúng là F.
Áp dụng hệ thức lượng trong tam giác vuông ABO:
\(OB^2=OH.OA\)
QE là tiếp tuyến \(\Rightarrow\Delta QEO\) vuông tại E, áp dụng hệ thức lượng:
\(OE^2=OF.OQ\)
Mà \(OB=OE=R\)
\(\Rightarrow OH.OA=OF.OQ\Rightarrow\dfrac{OA}{OQ}=\dfrac{OF}{OH}\)
Xét hai tam giác AOF và QOH có:
\(\left\{{}\begin{matrix}\dfrac{OA}{OQ}=\dfrac{OF}{OH}\\\widehat{FOH}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAF\sim\Delta QOH\left(g.g\right)\)
\(\Rightarrow\widehat{AFO}=\widehat{QHO}=90^0\)
Hay \(AF\perp QO\) tại F
Mà \(DE\perp QO\) cũng tại F
\(\Rightarrow3\) điểm A, D, E thẳng hàng