Các câu hỏi tương tự
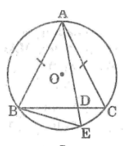
Cho đường tròn (O) và hai dây cung AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt (O) ở E. Chứng minh A B 2 = A D . A E
Cho đường tròn O và hai dây cung AB=AC Qua A vẽ một cát tuyến cắt dây BC tại D và cắt đường tròn O tại E Chứng minh AB²=AD.AE
Cho (O) và 2 dây cung AB, AC bằng nhau. Qua A vẽ 1 cát tuyến cắt dây BC ở D và cắt (O) ở E. Chứng minh AB2 = AD.AE
cho đường tròn tâm O . 2 dây AB,AC bằng nhau. Qua A vẽ các tuyến cắt dây BC ở D, cắt đường tròn O ở E. CMR :\(AB^2=AD.AE\)
Cho (O) và 2 dây AB,AC bằng nhau. Qua A vẽ cát tuyến cắt dây BC ở D và cắt (O) ở E. CMR
\(AB^2=AD.AE\)
Cho điểm A nằm ngoài đường tròn (O,R) với OARsqrt{2}Đường tròn tâm I đường kính OA cắt đường tròn (O) ở B và C.1) Chứng minh AB,AC là hai tiếp tuyến của đường tròn (O) và tính độ dài của AB, AC theo R2) Tứ giác ABOC là hình gì? Vì sao? 3) Đường thẳng OA cắt đường tròn (O) ở D và E ( D nằm giữa A và O). Kẻ cát tuyến AMN của đường tròn (O). Chứng minh AD.AEAM.AN hằng số 4) Khi cát tuyến AMN quay quanh A thì trung điểm K của đoạn MN di động trên đường cố định nào? Hãy chứng minh điều ấy5) Cát...
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O,R) với OA=R\(\sqrt{2}\)Đường tròn tâm I đường kính OA cắt đường tròn (O) ở B và C.
1) Chứng minh AB,AC là hai tiếp tuyến của đường tròn (O) và tính độ dài của AB, AC theo R
2) Tứ giác ABOC là hình gì? Vì sao?
3) Đường thẳng OA cắt đường tròn (O) ở D và E ( D nằm giữa A và O). Kẻ cát tuyến AMN của đường tròn (O). Chứng minh AD.AE=AM.AN= hằng số
4) Khi cát tuyến AMN quay quanh A thì trung điểm K của đoạn MN di động trên đường cố định nào? Hãy chứng minh điều ấy
5) Cát tuyến AMN cắt BC ở J. Chứng minh rằng O,K,J,I cùng nằm trên một đường tròn và AJ.AK=AB2
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm (O). Từ B và C vẽ hai tiếp tuyến của đường tròn, hai tiếp tuyến này cắt nhau ở D. Qua D vẽ một cát tuyến sonng song với AB, cát tuyến này cắt đường tròn tại các điểm M và N và cắt cạnh AC tai I
a) Chứng minh tứ giác OBDC nội tiếp đường tròn (O)
b) Chứng minh I là trung điểm của dây MN
Cho điểm A nằm ngoài đường tròn (O).Từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE tới đường tròn (B,C là hai tiếp điểm;D nằm giữa A&E).Gọi H là giao điểm của AO và BCa,Chứng minh rằng :ABOC là tứ giác nội tiếpb,Chứng minh rằng :AH.AOAD.AEc,Tiếp tuyến tại D của đường tròn (O)cắt AB,AC theo thứ tự tại I và K.Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AB tại P và cắt tia AC tại Q.Chứng minh rằng IP+KQPQ
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O).Từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE tới đường tròn (B,C là hai tiếp điểm;D nằm giữa A&E).Gọi H là giao điểm của AO và BC
a,Chứng minh rằng :ABOC là tứ giác nội tiếp
b,Chứng minh rằng :AH.AO=AD.AE
c,Tiếp tuyến tại D của đường tròn (O)cắt AB,AC theo thứ tự tại I và K.Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AB tại P và cắt tia AC tại Q.Chứng minh rằng IP+KQ>=PQ
Cho đg tròn (0) 2 dây AB,AC bằng nhau,qua A vẽ cát tuyến cắt dây BC tại D và cắt dg tròn tại E. CMR: AB bình phương = AD.AE