a, HS tự chứng minh
b, ∆IAC:∆IDB (g.g)
c, Sử dụng kết quả câu b)

a, HS tự chứng minh
b, ∆IAC:∆IDB (g.g)
c, Sử dụng kết quả câu b)
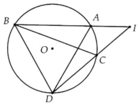
Cho đường tròn (O) và điểm I không nằm trên (O). Từ điểm I kẻ hai dây cung AB và CD ( A nằm giữa I và B; C nằm giữa I và D ) a, So sánh các cặp góc ACI và ABD, CAI và CDB b, CM tam giác IAC đồng dạng với tam giác IDB c, CM IA.IB = IC.ID
Cho đường tròn (O) và điểm I không nằm trên (O). Từ điểm I kẻ hai dây cung AB và CD ( A nằm giữa I và B; C nằm giữa I và D )
a, So sánh các cặp góc ACI và ABD, CAI và CDB
b, CM tam giác IAC đồng dạng với tam giác IDB
c, CM IA.IB = IC.ID
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Tích IA.IB bằng
A. ID.CD
B. IC.CB
C. IC.CD
D. ID.ID
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Tích IA.IB bằng
A. ID.CD
B. IC.CB
C. IC.CD
D. ID.ID
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D). Tích IA.IB bằng
A. ID.CD
B. IC.CB
C. IC.CD
D. IC.ID
Cho đường tròn (O) và điểm I nằm ngoài (O) . Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Cặp góc nào sau đây bằng nhau?
A. A C I ^ ; I B D ^
B. C A I ^ ; I B D ^
C. A C I ^ ; I D B ^
D. A C I ^ ; I A C ^
Cho đường tròn O bán kính R và hai điểm A, B nằm trên đường tròn (AB không là đường kính). Các tiếp tuyến tại A, B của đường tròn cắt nhau tại M. Kẻ cát tuyến MCD với đường tròn (C nằm giữa M và D)
a, Chứng minh các tam giác MBC và MDB đồng dạng
b, Chứng minh tứ giác MAOB là nội tiếp
c, Khi AB = R 3 , tính bán kinh đường tròn ngoại tiếp tứ giác MAOB theo R
d, Kẻ dây AE của (O) song song với MD. Nối BE cắt MD tại I. Chứng minh I là trung điểm của CD
Cho điểm M nằm ngoài đường tròn ( O ) . Kẻ hai tiếp tuyến MA ; MB đến đướng tròn ( O ) ( A , B là các tiếp điểm ) . Gọi I là điểm nằm giữa A và B trên đoạn AB . Vẽ dây BN của đường tròn song song với MI . Gọi C là điểm nằm chính giữa cung lớn BN , D là điểm nằm chính giữa cung nhỏ BN . Vẽ hai dây CE và DF của đường tròn cùng đi qua I . Chứng minh rằng MEIF là tứ giác nội tiếp .
1) Cho đường tròn (0) (0 là tâm). Từ điểm S ở ngoài đường tròn (0) kẻ các tiếp tuyển SA và SB với (0) (A, B là các tiếp điểm). Kẻ cát tuyến SCD không đi qua tâm O (C nằm giữa S và D). Gọi I là trung điểm của CD.
a) Chứng minh các điểm S, A, I, O, B cùng nằm trên một đường tròn.
b) Chứng minh SI là đường phân giác của góc AIB.
c) Gọi M là giao điểm của hai đường thẳng SO và AB; N là giao điểm của hai đường thẳng SD và AB. Chứng minh MC.ND = NC.MD.