Question

Cho đường tròn (O), dây AB=24cm, dây AC=20cm, góc BAC < 90 độ và điểm O nằm trong

tam giác ABC. Gọi M là trung điểm AC. Khoảng cách từ M đến AB bằng 8cm.
a. Chứng minh tam giác ABC cân tại C
b. Tính bán kính đường tròn.

Answer 1

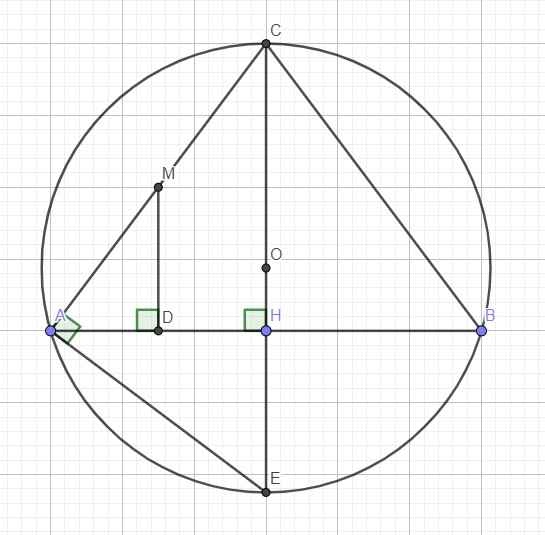
\(AM=\dfrac{1}{2}AC=10\left(cm\right)\)

Kẻ \(MD\perp AB\Rightarrow MD=8\left(cm\right)\)

Kẻ \(CH\perp AB\Rightarrow MD||CH\Rightarrow\) MD là đường trung bình tam giác ACH

\(\Rightarrow MD=\dfrac{1}{2}CH\Rightarrow CH=2MD=16\left(cm\right)\)

Áp dụng định lý Pitago cho tam giác vuông ACH:

\(AH=\sqrt{AC^2-CH^2}=12\left(cm\right)\)

\(\Rightarrow AH=\dfrac{1}{2}AB\Rightarrow H\) đồng thời là trung điểm AB

\(\Rightarrow\Delta ABC\) cân tại C

b.

Do tam giác ABC cân tại C \(\Rightarrow O\in CH\)

Kéo dài CH cắt đường tròn tại E (E khác C) \(\Rightarrow CE\) là đường kính

\(\Rightarrow\widehat{CAE}\) là góc nội tiếp chắn nửa đường tròn hay tam giác CAE vuông tại A

Áp dụng hệ thức lượng:

\(AC^2=CH.CE\Rightarrow CE=\dfrac{AC^2}{CH}=25\left(cm\right)\)

\(\Rightarrow R=\dfrac{1}{2}CE=12,5\left(cm\right)\)

Answer 2