Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)
Suy ra: OC ⊥ AB

Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)
Suy ra: OC ⊥ AB
Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng: OC là tia phân giác của góc AOB
Đề bài:Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM=BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:
a, OC là tia phân giác của góc AOB.
b, OC vuông góc AB.
Cho đường tròn (O) và hai bán kính OA và OB vuông góc với nhau. Gọi M và N là hai
điểm trên cung nhỏ AB sao cho AM = BN và C là giao điểm của hai đường thẳng AM và BN.
Chứng minh rằng: AB ⊥ OC.
cho đường tròn tâm o có bán kính OA và OB . Trên cung nhỏ AB lấy các điểm D và E sao cho AD=BE . gọi I là giao điểm của AM và BN .
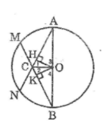
CHỨNG MINH a,OI là tia phân giác của góc AOB b,OI vuông góc AB mn giải hộ mình với ạ, vẽ hình càng tốtCho nửa đường tròn tâm O đường kính AB vẽ OC vuông góc với AB, nằm trên cung nhỏ BC lấy M tùy ý, lấy H là hình chiếu của C trên AM
a) Chứng minh tam giác HCM vuông cân
b) Gọi I là giao điểm của CM với BO, MI cắt nửa đường tròn tâm O tại D. Chứng minh CM//BD
c) Tìm vị trí M trên BC để HC=HO
d) Gọi N là giao điểm của AM và OC. Khi M di động trên cung nhỏ BC thì trung điểm K của BN di động trên đường nào vì sao ?
Cho đường tròn (O),các bán kính OM,ON.Trên cung nhỏ MN lấy các điểm A và B sao cho AM=BN.Gọi C là giao điểm của các đường thẳng AM và BN.Chứng minh rằng:
a)OC là tia phân giác của góc MON
b)OC vuông góc với MN
Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.
Trên nửa đường tròn tâm O đường kính AB lấy hai điểm M và N sao cho các cung AM ,MN,BN bằng nhau . Gọi P là giao điểm cảu AM và BN , H là giao điểm của AN với BM . Cmr
a, Tứ giác AMNB là hình thang cân
b, PH vuông góc với AB . Từ đó suy ra P, H , O thẳng hàng
Cho đường tròn (O) đường kính AB, C là điểm cố định chính giữa cung AB, M là 1 điểm di động trên cung nhỏ AC. Trên MB lấy N sao cho BN=AM. Chứng minh rằng khi M di động thì đường thẳng qua N vuông góc với MB luuon đi qua 1 điểm cố định.