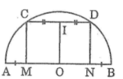
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.











