Các câu hỏi tương tự
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
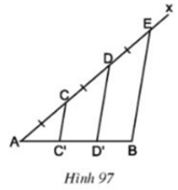
Cho đoạn thẳng AB, kẻ tia Ax bất kỳ, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C, D kẻ đường thẳng song song với BE. Chứng minh rằng đoạn thẳng AB bị chia ra ba phân bằng nhau.
Cho đường thẳng AB, kẻ tia Ax bất kì.Trên Ax lấy các điểm C,D,E sao cho AC=CD=DE.Qua C,D kẻ các đường thẳng song song với BE.CMR: đoạn thẳng AB bị chia thành 3 phần bằng nhau
Cho đoạn thẳng AB. Kẻ tia Ax bất kỳ. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE. Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB cắt AB lần lượt tại C', D'. Chứng minh: AC' = C'D' = D'B
Cho xAy90độ Trên tia Ax lấy các điểm B và C. Qua B và C vẽ hai đường thẳng song song cắt tia Ay ở D và E, qua E vẽ đường thẳng song song với CD, cắt tia Ax ở F.a) Chứng minh AB/ACAC/AF. Từ đó suy ra AC2ABxAFb) Qua B, kẻ đường thẳng song song CD cắt Ay ở M. Trên CF lấy điểm N sao cho CNDM. Gọi O là giao điểm của CD cà MN. Chứng minh: OM.ADAC.ON (Không sử dụng kiến thức tam giác đồng dạng).
Đọc tiếp
Cho xAy<90độ Trên tia Ax lấy các điểm B và C. Qua B và C vẽ hai đường thẳng song song cắt tia Ay ở D và E, qua E vẽ đường thẳng song song với CD, cắt tia Ax ở F.
a) Chứng minh AB/AC=AC/AF. Từ đó suy ra AC2=ABxAF
b) Qua B, kẻ đường thẳng song song CD cắt Ay ở M. Trên CF lấy điểm N sao cho CN=DM. Gọi O là giao điểm của CD cà MN. Chứng minh: OM.AD=AC.ON (Không sử dụng kiến thức tam giác đồng dạng).
Các bạn của minh và các bạn trên online math cố gắng giúp mình mấy bài này nha ai giúp được bài gì cũng được cảm ơn nhiều lắmToán 8 hình họcBài : đường thẳng song song với một đường thẳng cho trướcBài 1 . cho đoạn thẳng AB .Kẻ tia Ax bất kì . Trên tia Ax lấy các điểm C,D,E,F sao cho AC CD DE EF . Kẻ đoạn thẳng FB . Qua C, D,E kẻ CC’ , DD’ , EE’ song song với FB ( C’ ,D’ ,E’ thuộc đoạn thẳng AB )a, chứng minh AC’ C’D’ D’E’ E’B ( bằng hai cách khác nhau )b, cho DD’ 3 cm . Tính CC’ , FB (bằng ha...
Đọc tiếp
Các bạn của minh và các bạn trên online math cố gắng giúp mình mấy bài này nha ai giúp được bài gì cũng được cảm ơn nhiều lắm
Toán 8 hình học
Bài : đường thẳng song song với một đường thẳng cho trước
Bài 1 . cho đoạn thẳng AB .Kẻ tia Ax bất kì . Trên tia Ax lấy các điểm C,D,E,F sao cho AC = CD = DE =EF . Kẻ đoạn thẳng FB . Qua C, D,E kẻ CC’ , DD’ , EE’ song song với FB ( C’ ,D’ ,E’ thuộc đoạn thẳng AB )
a, chứng minh AC’ = C’D’= D’E’= E’B ( bằng hai cách khác nhau )
b, cho DD’= 3 cm . Tính CC’ , FB (bằng hai cách khác nhau)
bài 2 .cho đoạn thẳng AB . hãy chia đoạn thẳng AB thành 4 đoạn thẳng bằng nhau ( bằng 2 cách khác nhau )
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F. a) Chứng minh ED/AD + BF/BC 1b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD OB.OC.Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.a) Chứng minh CF DKb) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vu...
Đọc tiếp
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Cho tam giác ABC biết AB=5cm, BC=10cm. Lấy điểm D trên cạnh AB sao cho AD=3cm. Qua D kẻ đường thẳng song song với BC cắt AC tại E
a.Tính độ dài DE
b. Qua C kẻ đường thẳng song song với AB cắt tia DE tại G. Chứng minh tam giác ADE đồng dạng với tam giác CGE và AD.AE=DB.DE
c. Đường thẳng BG cắt AC tại H. Chứng minh HC2 = HE. HA
1. Cho hình thoi ABCD có số đo góc A bằng 1200. Gọi O là giao điểm của hai đường chéo AC và BD. Trên tia BC lấy điểm M sao cho BM4/3BC. Đường thẳng AM cắt CD tại N. Trên các đoạn thẳng AB, AD lần lượt lấy các điểm E, F sao cho CE//NF. Tính số đo góc EOF2. Cho điểm D thay đổi trên cạnh BC của tam giác nhọn ABC (D khác B và C). Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại điểm N. Cũng từ D kẻ đường thẳng song song với AC cắt cạnh AB tại điểm M. Tìm vị trí của D để đoạn thẳng MN có độ dài...
Đọc tiếp
1. Cho hình thoi ABCD có số đo góc A bằng 1200. Gọi O là giao điểm của hai đường chéo AC và BD. Trên tia BC lấy điểm M sao cho BM=4/3BC. Đường thẳng AM cắt CD tại N. Trên các đoạn thẳng AB, AD lần lượt lấy các điểm E, F sao cho CE//NF. Tính số đo góc EOF
2. Cho điểm D thay đổi trên cạnh BC của tam giác nhọn ABC (D khác B và C). Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại điểm N. Cũng từ D kẻ đường thẳng song song với AC cắt cạnh AB tại điểm M. Tìm vị trí của D để đoạn thẳng MN có độ dài nhỏ nhất.
3.. ABCD là hình chữ nhật có AB //CD, AB = 2CB. Từ A kẻ đường thẳng vuông góc với đường chéo BD tại H. Trên HB lấy điểm K sao cho HK = HA. Từ K kẻ đường thẳng song song với AH cắt AB tại E. Lấy M trung điểm DE, tia AM cắt DB tại N, cắt DC tại P.
Tính tỷ số diện tích tam giác AND với diện tam giác PMD?









