Question

Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD. Tính khoảng cách từ I đến AB.

Answer 1

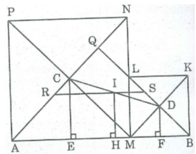
Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB

Suy ra: CE // DF // IH

IC = ID (gt)

Nên IH là đường trung bình của hình thang DCEF ⇒ IH = (DF + CE) / 2

Vì C là tâm hình vuông AMNP nên ∆ CAM vuông cân tại C

CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)

⇒ CE = 1/2 AM

Vì D là tâm hình vuông BMLK nên  ∆ DBM vuông cân tại D

DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân)

⇒ DF = 1/2 BM

Vậy CE + DF = 1/2 AM + 1/2 BM = 1/2 (AM + BM)= 1/2 AB = a/2

Suy ra: IH = (a/2) / 2 = a/4