Các câu hỏi tương tự
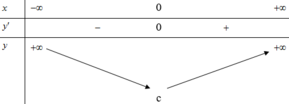
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho
a
0,
b
0,
a
≠
1,
b
≠
1
. Đồ thị hàm số
y
a
x
và
y
log
b
x
được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng? A.
a
1
;
0
b
1....
Đọc tiếp
Cho a > 0, b > 0, a ≠ 1, b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
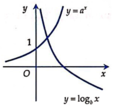
A. a > 1 ; 0 < b < 1.
B. 0 < a < 1 ; b > 1.
C. 0 < a < 1 ; 0 < b < 1.
D. a > 1 ; b > 1.
Hàm số
y
b
x
-
c
x
-
a
a
≠
0
;
a
,
b
,
c
∈
ℝ
có đồ thị như hình vẽ bên. Khẳng đị...
Đọc tiếp
Hàm số y = b x - c x - a a ≠ 0 ; a , b , c ∈ ℝ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A. a > 0, b > 0, c - ab < 0
B. a > 0, b > 0, c - ab > 0
C. a > 0, b > 0, c - ab = 0
D. a > 0, b < 0, c - ab < 0
Cho
a
0
,
b
0
,
b
≠
0
. Đồ thị các hàm số
y
a
x
và
y
log
b
x
cho như hình vẽ bên. Mệnh đề nào sau đây là đúng A. a1, 0b1 B. 1a0; b1 C. 0a1; 0b1 D. a1; b1
Đọc tiếp
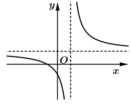
Cho a > 0 , b > 0 , b ≠ 0 . Đồ thị các hàm số y = a x và y = log b x cho như hình vẽ bên. Mệnh đề nào sau đây là đúng
A. a>1, 0<b<1
B. 1>a>0; b>1
C. 0<a<1; 0<b<1
D. a>1; b>1
Cho
0
a
≠
1
và
0
b
≠
1
. Đồ thị hàm số
y
a
x
và
y
log
b
x...
Đọc tiếp
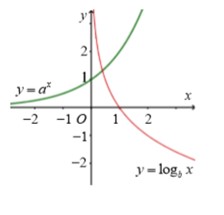
Cho 0 < a ≠ 1 và 0 < b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?

A. a >1, b >1
B. a >1, 0 <b <1
C. 0 <a <1, b >1
D. 0 <a <1, 0 <b <1
Cho hàm số
y
ax
3
+
bx
2
+
cx
+
d
(a,b,c,d là các hằng số,a≠0) có đồ thị như sau:Khẳng định nào sau đây là khẳng định đúng? A. abcd 0. B a–b+c+d 0. C. a–b+c+d 0. D. abcd 0.
Đọc tiếp
Cho hàm số y = ax 3 + bx 2 + cx + d (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:
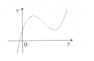
Khẳng định nào sau đây là khẳng định đúng?
A. abcd > 0.
B a–b+c+d < 0.
C. a–b+c+d > 0.
D. abcd = 0.
Đồ thị hàm số y ax3 + bx2 + cx + d (a, b, c, d là các hằng số thực và a ≠ 0) như hình vẽ. Khẳng định nào đúng A. b 0, c 0 B. b 0, c 0 C. b 0, c 0 D. b 0, c 0
Đọc tiếp
Đồ thị hàm số y = ax3 + bx2 + cx + d (a, b, c, d là các hằng số thực và a ≠ 0) như hình vẽ.
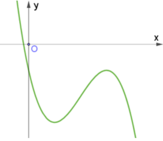
Khẳng định nào đúng
A. b > 0, c > 0
B. b < 0, c < 0
C. b < 0, c > 0
D. b > 0, c < 0
Cho hàm số
y
b
x
-
c
x
-
a
(a ≠ 0 và a,b,c ϵ ℝ) có đồ thị như hình bên dưới. Khẳng định nào dưới đây là đúng? A. a 0, c-ab 0 B. a 0,b 0,c-ab 0 C. a 0,b 0,c-ab 0 D. a 0,b 0,c-ab 0
Đọc tiếp
Cho hàm số y = b x - c x - a (a ≠ 0 và a,b,c ϵ ℝ) có đồ thị như hình bên dưới. Khẳng định nào dưới đây là đúng?
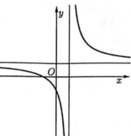
A. a > 0, c-ab < 0
B. a > 0,b > 0,c-ab > 0
C. a < 0,b> 0,c-ab < 0
D. a < 0,b < 0,c-ab > 0
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0