Đáp án A
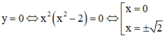
do đó hàm số cắt trục hoành tại 3 điểm phân biệt.
Đáp án A
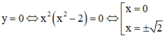
do đó hàm số cắt trục hoành tại 3 điểm phân biệt.
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y = x + 1 x 2 + m x + 1 có đồ thị (C). Tìm số nguyên dương nhỏ nhất m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt.
A. m = 2
B. m = 4
C. m = 3
D. m = 1
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
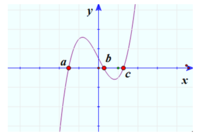
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
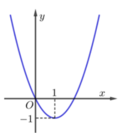
Cho hàm số y = a x 3 + b x 2 + c x + d có đạo hàm là hàm số y=f'(x) có đồ thị như hình vẽ bên.
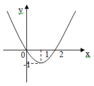
Biết rằng đồ thị hàm số y=f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
A. 2 3
B. 1
C. 3 2
D. 4 3
Cho hàm số y = ax 3 + bx 2 + cx + d có đạo hàm là hàm số y = f '(x) có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y = f(x)cắt trục tung tại điểm có tung độ bằng bao nhiêu?
A. 2 3 .
B. 1
C. 3 2 .
D. 4 3 .
Cho hàm số y = e a x 2 + b x + c đạt cực trị tại x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e. Tính giá trị của hàm số tại x=2?
A. y 2 = e 2
B. y 2 = 1 e 2
C. y 2 = 1
D.. y 2 = e
Cho hàm số y = e ax 2 + bx + c đạt cực trị tại x = 1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e 2 . Tính giá trị của hàm số tại x = 2
A. y 2 = 0
B. y 2 = e 2
C. y 2 = 1
D. y 2 = e
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1
D. -3
Cho hàm số y = x 3 + 3 x 2 + m có đồ thị (C) . Biết đồ thị (C) cắt trục hoành tại 3 điểm phân biệt A, B, C sao cho B là trung điểm của AC. Phát biểu nào sau đây đúng?
A. m ∈ 0 ; + ∞
B. m ∈ − ∞ ; − 4
C. m ∈ − 4 ; 0
D. m ∈ − 4 ; − 2
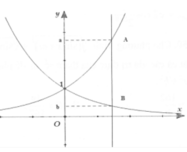
Cho đồ thị hàm số y = 2 x là đồ thị ( C 1 ) như hình vẽ, ( C 2 ) là đồ thị đối xứng của ( C 1 ) qua trục Oy. Một đường thẳng d song song với Oy cắt đồ thị ( C 1 ), ( C 2 ) tại 2 điểm A, B như hình vẽ có tung độ lần lượt là a, b. Giá trị nhỏ nhất của biểu thức P = 4 a 3 + b 3 - 3 a + b 2 a + 2 b - 3 là
A. 14
B. 0
C. 4
D. - 2