Ta có ME = MF => ΔEMF cân tại M
Ta có:
E M F ^ = 180 ° - C M A ^ - D M B ^ = 180 ° - 60 ° - 60 ° = 60 °
Từ đó MEF là tam giác cân có một góc bằng 60 ° nên nó là tam giác đều
Vậy EF = ME = MF = 2 a 3
Đáp án: A
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho điểm M thuộc đoạn thẳng AB sao cho MA 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Đặt MB a. Tính ME, MF theo a. A.
M
E
a
2
;
M
F
a
3
B.
M
E
M
F
2
a
3
C. ...
Đọc tiếp
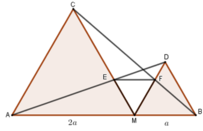
Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Đặt MB = a. Tính ME, MF theo a.
A. M E = a 2 ; M F = a 3
B. M E = M F = 2 a 3
C. M E = 2 a 3 ; M F = a 3
D. M E = M F = a 3
Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Đặt MA a, MB b. Tính ME, MF theo a và b. A.
M
E
a
b
b
+
a
;
M
F
a
b
+
a
B. ...
Đọc tiếp
Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Đặt MA = a, MB = b. Tính ME, MF theo a và b.
A. M E = a b b + a ; M F = a b + a
B. M E = M F = a b b + a
C. M E = b b + a ; M F = a b + a
D. M E = M F = a − b b + a
Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Tam giác MEF là tam giác gì? Chọn đáp án đúng nhất?
A. Tam giác MEF đều
B. Tam giác MEF cân tại M
C. Tam giác MEF cân tại N
D. Cả A, B, C đều sai
cho M thuộc AB vẽ về 1 phía các tam giác đều AMC VÀ BMD E là giao điểm AD VÀ MC , F là giao điểm BC VÀ MD MA=a, MB=b. tính ME,MF THEO a,b
Cho tam giác ABC . Qua A vẽ đường thẳng xy//BC . Trên cạnh BC lấy điểm D vẽ DE//AB, DF//AC(E,F thuộc xy).Gọi M là giao điểm của AB và DF. Gọi N là giao của AC và DE. Gọi O là giao của AD và CF. Chứng minh rằng:
a) 3 điểm B , O, E thẳng hàng b) 3 điểm M, O , N thẳng hàng
cho hbh ABCD. GỌI M,N lần lượt là trung điểm của AB và CD . Gọi E là giao của AN và DM , F là giao điểm của MC và BN . C/M
a, AD=MN
b, tứ giác BCNM , MENF là hbh
c, E, F và trung điểm của MN thẳng hàng
Cho hình bình hành ABCD .Gọi M,N lần lượt là trung điểm của AB và CD .Gọi E là giao điểm của AN và DM ,F là giao điểm của MC và BN .Chứng minh
a, AD=MN
b, Tứ giác BCNM ,MENF là hình bình hành
c, E,F và trung điểm của MN thẳng hàng
Cho tam giác ABC vuông tại A, có AB 12cm, AC 16cm. Kẻ đường cao AH và đường trung tuyến AD (H,D thuộc BC)a) Tính độ dài đoạn thẳng BC, ADb) Chứng minh AH2 HB.HCc) Qua A kẻ đương thẳng d vuông góc với AD, qua B kẻ đường thẳng d vuông góc với BA. Gọi M là giao điểm của d và d, E là hình chiếu của B trên AM. Chứng minh góc ABE góc BAD và tam giác ABC đồng dạng với tam giác EMBd) Gọi N là giao điểm của AD và MB, F là giao điểm của DM và AB. Chứng minh E, F, N thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB = 12cm, AC = 16cm. Kẻ đường cao AH và đường trung tuyến AD (H,D thuộc BC)
a) Tính độ dài đoạn thẳng BC, AD
b) Chứng minh AH2 = HB.HC
c) Qua A kẻ đương thẳng d vuông góc với AD, qua B kẻ đường thẳng d' vuông góc với BA. Gọi M là giao điểm của d và d', E là hình chiếu của B trên AM. Chứng minh góc ABE = góc BAD và tam giác ABC đồng dạng với tam giác EMB
d) Gọi N là giao điểm của AD và MB, F là giao điểm của DM và AB. Chứng minh E, F, N thẳng hàng.
Cho hình bình hành ABCD. Điểm E thuộc tia đối của AB, điểm F thuộc tia đối của CD sao cho AE=CF. Gọi M là giao điểm của AD và CE; N là giao điểm của AF và BC. Gọi O là giao điểm của MN và AC. Chứng minh: a) B, O, D thẳng hàng b) E, O, F thẳng hàng