Xét ΔCAB có KD//AB
nên ΔCDK đồng dạng với ΔCBA
=>\(\dfrac{S_{CDK}}{S_{CBA}}=\left(\dfrac{CD}{CB}\right)^2\)
=>\(S_{CBA}=16:\dfrac{CD^2}{CB^2}=16\cdot\dfrac{CB^2}{CD^2}\)
Xét ΔBED và ΔBAC có
góc BED=góc BAC
góc B chung
=>ΔBED đồng dạng với ΔBAC
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{BD}{BC}\right)^2\)
=>\(S_{ABC}=9\cdot\dfrac{BC^2}{BD^2}=16\cdot\dfrac{BC^2}{CD^2}\)
=>3/BD=4/CD
=>BC=7/3BD
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{3}{7}\right)^2=\dfrac{9}{49}\)
=>\(S_{BAC}=49\left(cm^2\right)\)









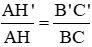 .
.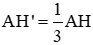 và diện tích tam giác ABC là 67,5 cm
và diện tích tam giác ABC là 67,5 cm

