Question

Cho \(\Delta ABC\) không có góc tù. CMR: nếu \(tanB=cotC\) thì \(\Delta ABC\) vuông

Answer 1

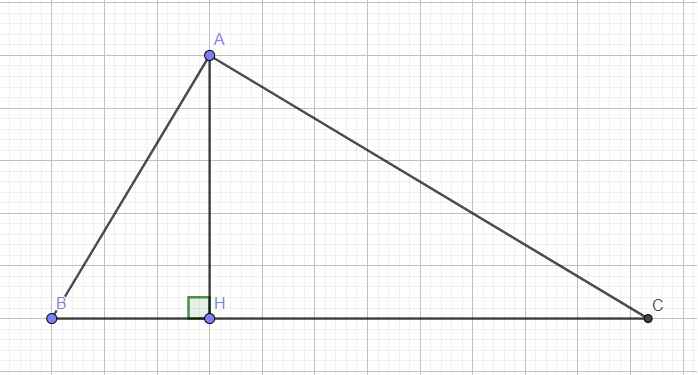
Kẻ đường cao AH

Trong tam giác vuông ABH ta có:

\(tanB=\dfrac{AH}{BH}\)

Trong tam giác vuông ACH:

\(cotC=\dfrac{CH}{AH}\)

\(\Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\) \(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)

Xét hai tam giác vuông ABH và CAH:

\(\left\{{}\begin{matrix}\dfrac{AH}{CH}=\dfrac{BH}{AH}\\\widehat{AHB}=\widehat{CHA}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta ABH\sim\Delta CAH\left(c.g.c\right)\)

\(\Rightarrow\widehat{B}=\widehat{CAH}\)

\(\Rightarrow\widehat{A}=\widehat{BAH}+\widehat{CAH}=\widehat{BAH}+\widehat{B}=90^0\)

\(\Rightarrow\Delta ABC\) vuông tại A (đpcm)

Answer 2