Các câu hỏi tương tự
Câu 1: Cho tam giác ABC cân tại A.Gọi M là trung điểm của cạnh BC
a) Chứng minh \(\Delta ABM=\Delta ACM\)
b) Kẻ MD \(\perp\)AB (D \(\varepsilon\)AB), ME \(\perp\)AC ( E \(\varepsilon\)AC)
Chứng minh rằng MD= ME
c) Cho AM = 5 cm, MD = 3 cm, Tính độ dài đoạn thẳng AD?
Cho Delta ABC cân tại A, lấy điểm M là trung điểm của cạnh BC. Trên tia đối của MA lấy điểm D sao cho MA MD
Chứng minh:
a) Delta AMB và Delta DMC
b) AC // BD
c) Kẻ AH perp BC, DK perp BC ( H, K in BC ) Chứng minh BK CH
Đọc tiếp
Cho \(\Delta ABC\) cân tại A, lấy điểm M là trung điểm của cạnh BC. Trên tia đối của MA lấy điểm D sao cho MA = MD
Chứng minh:
a) \(\Delta AMB\) và \(\Delta DMC\)
b) AC // BD
c) Kẻ AH \(\perp\) BC, DK \(\perp\) BC ( H, K \(\in\) BC ) Chứng minh BK = CH
cho \(\Delta ABC\) cân tại A.Kẻ BH \(\perp\)BC tại H
a.chứng minh \(\Delta ABH=\Delta ACH\)
b.vẽ trung tuyến CN.Gọi G là giao điểm của AH và CN.Chứng minh G là trọng tâm của \(\Delta ABC\)
c.từ H kẻ HE song song với AB (E thuộc AC).Chứng minh ba điểm B, G,E thẳng hàng
Câu 1. Cho tam giác ABC vuông tại A (ABAC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AMABa) Chứng minh: DBDMb) Gọi E là giao điểm AB và MD. Chứng minh Delta BEDDelta MCDc) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàngCâu 2 . Cho Delta ABCcó ABAC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BABEa) Chứng minh: DADEb) Tia ED cắt BA tại F. Chứng minh Delta DAFDelta DECc) Gọi H là trung diểm của FC. Chứng minh ba điểm B,D,H thẳng hàng...
Đọc tiếp
Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=AB
a) Chứng minh: DB=DM
b) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)
c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàng
Câu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BE
a) Chứng minh: DA=DE
b) Tia ED cắt BA tại F. Chứng minh \(\Delta DAF=\Delta DEC\)
c) Gọi H là trung diểm của FC. Chứng minh ba điểm B,D,H thẳng hàng
Câu 3. Cho \(\Delta ABC\)cân tại A. Kẻ AH vuông góc với BC (\(H\in BC\))
a) Chứng minh: HB=HC
b) Kẻ \(HD\perp AB\left(D\in AB\right)\)và \(HE\perp AC\left(E\in AC\right)\). Chứng minh \(\Delta HDE\)cân
Câu 4. Cho tam giác ABC vuông tại B, đường phân giác \(AD\left(D\in BC\right)\). Kẻ DE vuông góc với \(AC\left(E\in AC\right)\)
a) Chứng minh: \(\Delta ABD=\Delta AED;\)
b) BE là đường trung trực của đoạn thẳng AD
c) Gọi F là giao điểm của hai đường thẳng AB và ED Chứng minh BF=EC
Cho tam giác ABC cân tại A, Gọi M là trung diểm của cạnh Bc
a) chứng minh: $\Delta$Δ ABM = $\Delta$ΔACM
b) từ M vẽ MH vuông góc với AB và MK vuông góc với AC. chứng minh BH=CK
c) Từ B vẽ BP vuông góc với AC, BP cắt MH tại I. chứng minh $\Delta$ΔIBM cân
Cho Delta ABC cân tại A,đường cao BH trên đáy BC lấy điểm M,vẽ MDperp AB,MEperp AC,MFperp BH.
a) Chứng minh ME HF b) Delta DBMDelta FMB
c)Khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.
d)Trên tia đối của tia CA lấy điểm K sao cho KC EH.Chứng minhtrung điểm của KD nằm trên cạnh BC.
Đọc tiếp
Cho \(\Delta ABC\) cân tại A,đường cao BH trên đáy BC lấy điểm M,vẽ \(MD\perp AB,ME\perp AC,MF\perp BH\).
a) Chứng minh ME = HF b) \(\Delta DBM=\Delta FMB\)
c)Khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.
d)Trên tia đối của tia CA lấy điểm K sao cho KC = EH.Chứng minhtrung điểm của KD nằm trên cạnh BC.
Bài 5: Cho tam giác ABC có ABAC, Kẻ BDperpAC tại D, Kẻ CEperpAB tại E, BD cắt CE tại Ha) Chứng minh: DeltaABD DeltaACEb) Chứng minh: DeltaBCD DeltaCBEc) Chứng minh: DeltaBCD DeltaCHDd) Chứng minh: AH là tia phân giác của góc BAC
Đọc tiếp
Bài 5: Cho tam giác ABC có AB=AC, Kẻ BD\(\perp\)AC tại D, Kẻ CE\(\perp\)AB tại E, BD cắt CE tại H
a) Chứng minh: \(\Delta\)ABD = \(\Delta\)ACE
b) Chứng minh: \(\Delta\)BCD = \(\Delta\)CBE
c) Chứng minh: \(\Delta\)BCD = \(\Delta\)CHD
d) Chứng minh: AH là tia phân giác của góc BAC
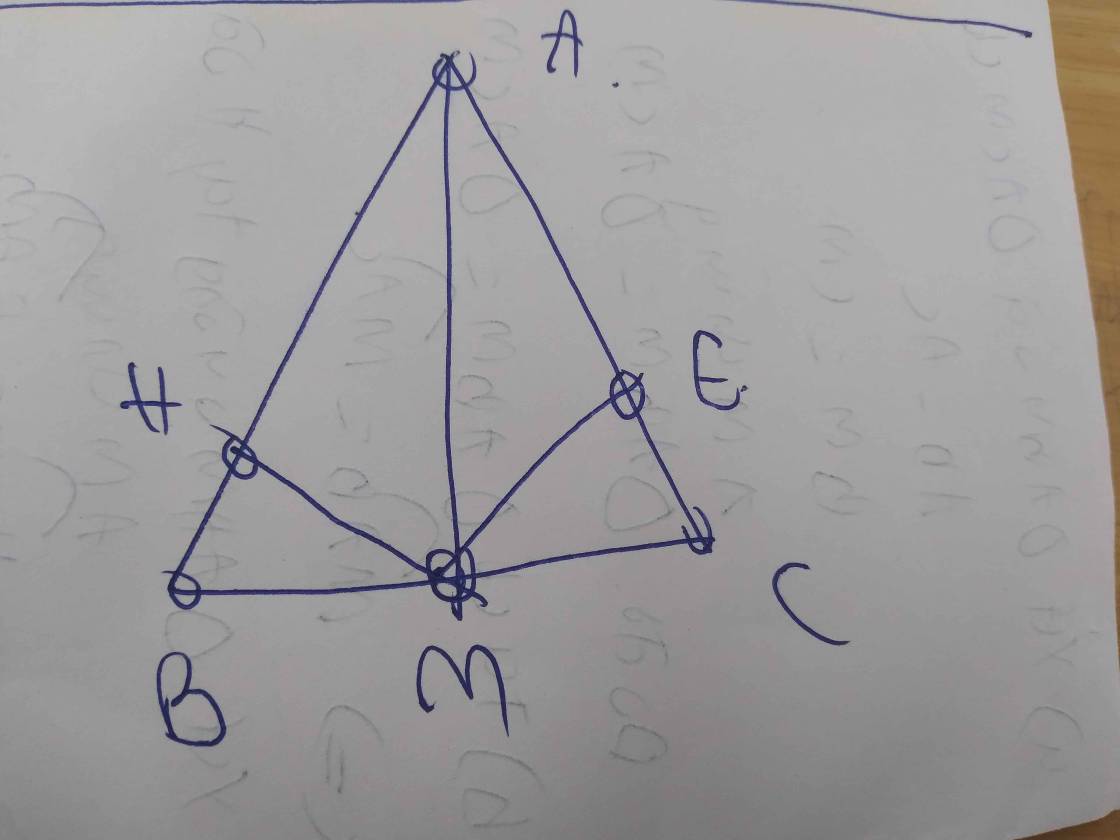
cho tam giác ABC cân tại A , M là trung điểm của BC . Tu M kẻ \(ME\perp AB\)tại E , \(MF\perp AC\)tại F. Chứng minh :
a, \(\Delta BEM=\Delta CFM\)
b,AM là trung trực của EF
c, Từ B kẻ đường thẳng vuông góc với AB tại D . chung minh : A , M , D thẳng hàng
Cho tam giác ABC cân tại A, Gọi M là trung diểm của cạnh Bc
a) chứng minh: \(\Delta\) ABM = \(\Delta\)ACM
b) từ M vẽ MH vuông góc với AB và MK vuông góc với AC. chứng minh BH=CK
c) Từ B vẽ BP vuông góc với AC, BP cắt MH tại I. chứng minh \(\Delta\)IBM cân
Cho tam giác ABC có ABAC gọi M là trung điểm của BCa) Chứng minh rằng: Delta ABMDelta ACMb)Từ M kẻ MHperpAC tại H. Trên tia đối của tia HM lấy điểm D sao cho H là trung điểm của MD. CHứng minh rằng CA là tia phân giác của widehat{MCD}c) Đường thẳng qua H và song song vs AD cắt Cd tại E. Chứng minh rằng: HEperpCDMong các bn giúp đỡ nha^_^ ( hai ý đầu mik lm đc òi còn ý c thoy mong các sư huynh sư tỷ giúp đợ ạ)^_^^
Đọc tiếp
Cho tam giác ABC có AB=AC gọi M là trung điểm của BC
a) Chứng minh rằng: \(\Delta ABM=\Delta ACM\)
b)Từ M kẻ MH\(\perp\)AC tại H. Trên tia đối của tia HM lấy điểm D sao cho H là trung điểm của MD. CHứng minh rằng CA là tia phân giác của \(\widehat{MCD}\)
c) Đường thẳng qua H và song song vs AD cắt Cd tại E. Chứng minh rằng: HE\(\perp\)CD
Mong các bn giúp đỡ nha^_^ ( hai ý đầu mik lm đc òi còn ý c thoy mong các sư huynh sư tỷ giúp đợ ạ)^_^^