Các câu hỏi tương tự
Cho △DDEF vuông tại D( DF > DE) .Vẽ đường tròn tâm O đường kính DF, cắt EF tại H.
a) Chứng minh DH ⊥ EF (1đ)
b) Từ O vẽ OK vuông góc với HF tại K .Cho OF = 5cm và HF = 8cm. Chứng minh K là trung điểm của HF và tính OK (1,5đ)
c) Chứng minh HE . HF = 4. OK2 (0,5đ)
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao BE, CF cắt nhau tại H
a) chứng minh tứ giác AEHF, BCEF nội tiếp
b) Đường thẳng EF và BC cắt nhau tại I, vẽ tiếp tuyến ID của đường tròn O. Chứng minh ID^2=IB*IC
c) DE, DF cắt đường tròn O tại M, N. Chứng minh MN//EF
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao BE, CF cắt nhau tại H
a) chứng minh tứ giác AEHF, BCEF nội tiếp
b) đường thẳng EF và BC cắt nhau tại I, vẽ tiếp tuyến ID với đường tròn ( D là tiếp điểm, D thuộc cung BC nhỏ). Chứng minh: ID^2=IB*IC
c) DE, DF cắt đường tròn (O) tại M,N. Chứng minh MN//EF
cho tam giác ABC nhọn. Vẽ đường tròn tâm O dường kính BC cắt 2 cạnh AB,AC lần lượt tại E và D; BD và CE cắt nhau tại H
a,chứng minh rằng: H vuông góc với BC
b,chứng minh: bốn điểm A,H,E,D cùng thuộc 1 đường tròn và DE<BC
c,gọi M,N lần lượt chân các đường vuông góc kẻ từ B và C đến DE. Chứng minh rằng ME=ND
Cho tam giác DEF vuông tại D ;DE>DF,đường cao DH.Trên nửa mp bờ EF chứa D vẽ nửa đường tròn đường kính DH cắt DE tại K,vẽ nửa đường tròn đường kính HF cắt DF tại I
a,CMR DKHD là hcn
b,CM DK.DE=DI.DF
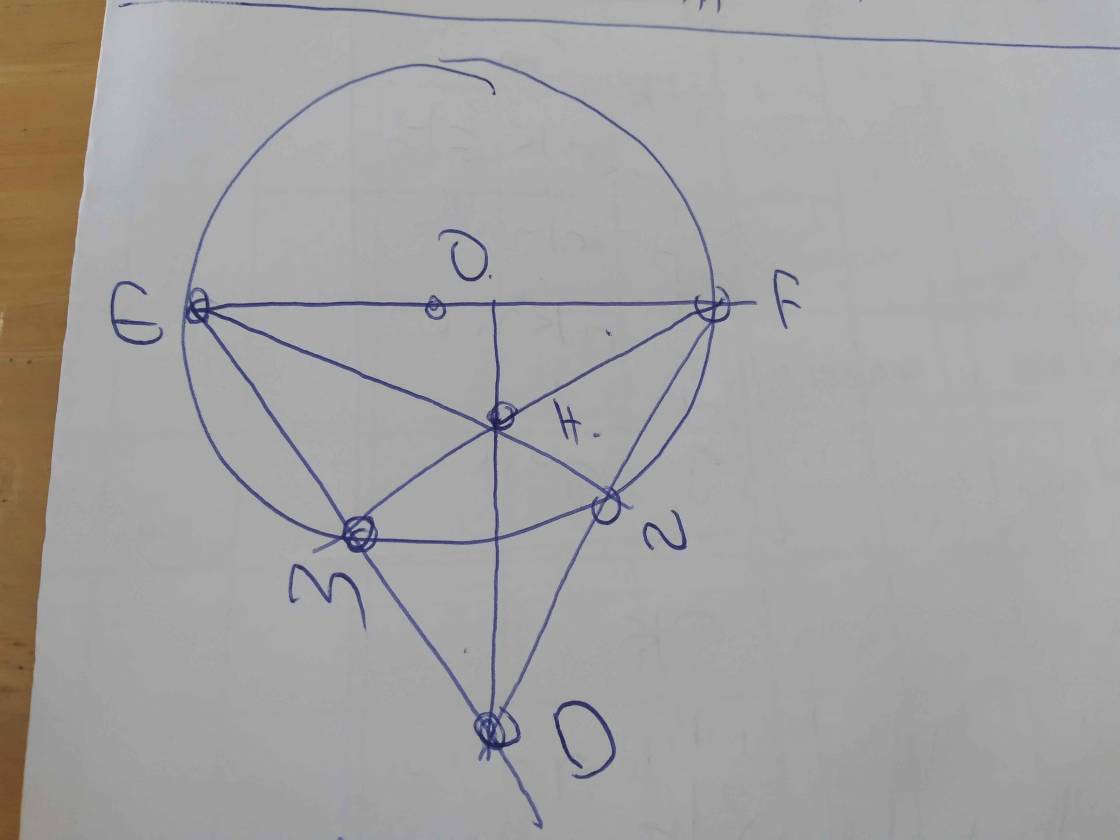
Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt cạnh AC cad AB lần lượt tại E và F. Gọi H là giao điểm của BE cà CF. AH cắt cạnh BC tại D.
a) Chứng minh các tứ giác BFEC, BFHD, CEHD nội tiếp đường tròn.
b) Qua O kẻ đường thẳng vuông góc với BC cắt DE và DF lần lượt tại G và I. Chứng minh BGCI là hình thoi
Cho tam giác ABC (ABAC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại E, F. Gọi H là giao điểm của BE và CF. D là giao điểm của AH và BC.a) Chứng minh : AD vuông góc BCb) Chứng minh EFDO là tứ giác nội tiếpc) Trên tia đối của tia DE lấy điểm L sao cho DL DF. Tính số đo góc BLCd) Gọi R, S lần lượt là hình chiếu của B,C lên EF. Chứng minh DE + DF RS và AH.ADAE.AC
Đọc tiếp
Cho tam giác ABC (AB<AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại E, F. Gọi H là giao điểm của BE và CF. D là giao điểm của AH và BC.
a) Chứng minh : AD vuông góc BC
b) Chứng minh EFDO là tứ giác nội tiếp
c) Trên tia đối của tia DE lấy điểm L sao cho DL = DF. Tính số đo góc BLC
d) Gọi R, S lần lượt là hình chiếu của B,C lên EF. Chứng minh DE + DF = RS và AH.AD=AE.AC
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R) (AB AC). Gọi H là giao điểm của ba đường cao BE, CF và ADa) Chứng minh: Tứ giác BFEC và AFHE nội tiếp.b) Vẽ đường kính AK của đường tròn (O). Chứng minh: AK.AD AB.ACc) Gọi N là giao điểm của OA và EF. Chứng minh: tứ giác NHDK nội tiếp.d) Gọi Q, V lần lượt là hình chiếu của H lên EF và DF, QV cắt AD tại I, EI cắt DF tại S. Chứng minh: SI IE Giúp mình câu d với
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R) (AB < AC). Gọi H là giao điểm của ba đường cao BE, CF và AD
a) Chứng minh: Tứ giác BFEC và AFHE nội tiếp.
b) Vẽ đường kính AK của đường tròn (O). Chứng minh: AK.AD AB.AC
c) Gọi N là giao điểm của OA và EF. Chứng minh: tứ giác NHDK nội tiếp.
d) Gọi Q, V lần lượt là hình chiếu của H lên EF và DF, QV cắt AD tại I, EI cắt DF tại S. Chứng minh: SI = IE
Giúp mình câu d với
Cho tam giác DEF có ba góc nhọn nội tiếp đường tròn (O) với DE DF và DH là đường cao. Kẻ phân giác góc D cắt (O) tại P. Qua F kẻ tiếp tuyến với (O) cắt EP kéo dài ở K.a) Chứng minh DP là tia phân giác của góc ODHb) PO cắt EF tại M và cắt (O) tại Q. Kẻ OG⊥QFOG⊥QF (G∈QF∈QF) Chứng minh tứ giác OMFG nội tiếp một đường tròn tiếp xúc với đường tròn (O) tại F.c) Chứng minh rằng: EP 2OG.d) Chứng minh rằng: OG.KF KP.MF.
Đọc tiếp
Cho tam giác DEF có ba góc nhọn nội tiếp đường tròn (O) với DE < DF và DH là đường cao. Kẻ phân giác góc D cắt (O) tại P. Qua F kẻ tiếp tuyến với (O) cắt EP kéo dài ở K.
a) Chứng minh DP là tia phân giác của góc ODH
b) PO cắt EF tại M và cắt (O) tại Q. Kẻ OG⊥QFOG⊥QF (G∈QF∈QF) Chứng minh tứ giác OMFG nội tiếp một đường tròn tiếp xúc với đường tròn (O) tại F.
c) Chứng minh rằng: EP = 2OG.
d) Chứng minh rằng: OG.KF = KP.MF.
cho nửa đường tròn tâm (O) đường kính EF. Vẽ tia Ot vuông góc với EF. Ot cắt nửa đường tròn tại I. Lấy điểm A trên tia Ot sao cho IA=IO. VẼ hai tiếp tuyến AP và AQ với nửa dường tròn cắt EF lần lượt tại B,C.Từ điểm S bất kỳ trên cung PQ, vẽ tiếp tuyến với nửa đg tròn; tiếp tuyến này cắt AB,AC tại H,K. Gọi M,N lần lượt là giao diểm của PQ với OH,OK.Chứng minh OMKQ nội tiếp