Chọn C
Ta có u 2 ; u 4 ; u 6 ; … ; u 20 lập thành cấp số nhân số hạng đầu u 2 = 9 ; q = 3 và có 10 số hạng nên
S = u 2 . 1 − 3 10 1 − 3 = 9. 3 10 − 1 2 = 9 2 ( 3 10 − 1 )
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho dãy số (
u
n
) xác định bởi
u
1
0
và
u
n
+
1
u
n
+
4
n
+
3
,
∀
n
⩾
2
. Biết :
l
i
m
u...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 0 và u n + 1 = u n + 4 n + 3 , ∀ n ⩾ 2 . Biết :
l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + 2 2018 n = a 2019 + b c với a,b,c là các số nguyên dương và b<2019. Tính giá trị S=a+b-c
A.S= -1
B.S=0
C.S=2017
D.S=2018
1) Tính \(S=-1+\dfrac{1}{10}-\dfrac{1}{10^2}+...+\dfrac{\left(-1\right)^n}{10^{n-1}}\)
2) Tính \(S=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{n-1}}\)
1, S=1/3-1/9+...+(-1)n+1/3 gt của tổng bằng:
2, S=1/3+1/32+..1/3n+.. Có gt là
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số
u
n
xác định bởi
u
1
321
và
u
n
+
1
u
n
-
3
với mọi
n
∈
N
*
. Tính tổng S của 125 số hạng đầu tiên của dãy số đó. A. S 16875 B. S 6...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 321 và u n + 1 = u n - 3 với mọi n ∈ N * . Tính tổng S của 125 số hạng đầu tiên của dãy số đó.
A. S = 16875
B. S = 63375
C. S = 63562,5
D. S = 16687,5
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
cho dãy số (un):\(\left\{{}\begin{matrix}u_1=\sqrt{3}+\sqrt{2}\\u_{n+1}=\left(\sqrt{3}-\sqrt{2}\right)u^2_n+\left(2\sqrt{6}-5\right)u_{n_{ }}+3\sqrt{3}-3\sqrt{2}\end{matrix}\right.\)
tìm lim(\(\Sigma^1_{i=1}\dfrac{1}{u_i+\sqrt{2}}\))
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số
a
b
c
¯
từ S. Tính xác suất để số được chọn thỏa mãn
a
≤
b
≤
c
.
Đọc tiếp
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số a b c ¯ từ S. Tính xác suất để số được chọn thỏa mãn a ≤ b ≤ c .
Cho dãy số (
u
n
) xác định bởi
u
1
0
và
u
n
+
1
u
n
+
4
n
+
3
,
∀
n
≥
1
. Biết
l
i...
Đọc tiếp
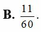
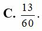
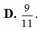
Cho dãy số ( u n ) xác định bởi u 1 = 0 và
u n + 1 = u n + 4 n + 3 , ∀ n ≥ 1 .
Biết
l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + u 2 2018 n = a 2019 + b c
với a, b, c là các số nguyên dương và b < 2019 .
Tính giá trị S=a+b-c.
