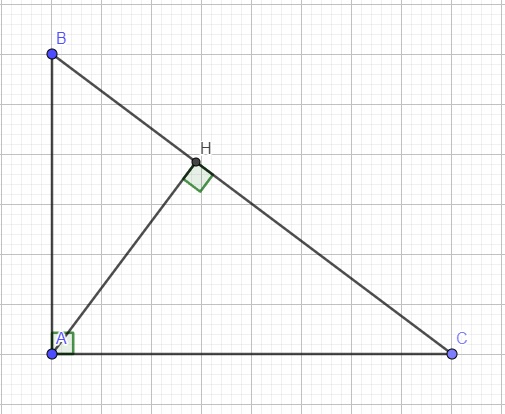
Xét hai tam giác ABC và HBA có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\) (1)
Áp dụng định lý Pitago trong tam giác vuông ABC:
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Thay vào (1): \(HB=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông ABH:
\(HA=\sqrt{AB^2-HB^2}=4,8\left(cm\right)\)