Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là: A. 39
c
m
2
B. 36
c
m
2
C. 18
c
m
2
D. 27
c
m
2
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là:
A. 39 c m 2
B. 36 c m 2
C. 18 c m 2
D. 27 c m 2
1.Cho tam giác ABCcân tại A có AB AC 100cm, BC 120cm. Hai đường cao AD, BE cắt nhau tại H.a)Tìm các tam giác đồng dạng với tam giác BDHb)Tình độ dài các đoạn: HD, AH, BH, EH2.Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Đường cao AH, đường phân giác BDa)Tình độ dài AD, DCb)Gọi I là giao điểm của AH và BD. C/m: AB.BI BD.HBc)C/m: Tam giác AID cân3.Cho hình thang cân ABCD (AB//CD), AB CD. Đường cao BH chia cạnh CD thành 2 đoạn DH 16cm, HC 9cm. Biết BD vuông góc BC.a)Tính đường chéo AC và...
Đọc tiếp
1.Cho tam giác ABCcân tại A có AB = AC = 100cm, BC = 120cm. Hai đường cao AD, BE cắt nhau tại H.a)Tìm các tam giác đồng dạng với tam giác BDHb)Tình độ dài các đoạn: HD, AH, BH, EH
2.Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Đường cao AH, đường phân giác BDa)Tình độ dài AD, DCb)Gọi I là giao điểm của AH và BD. C/m: AB.BI = BD.HBc)C/m: Tam giác AID cân
3.Cho hình thang cân ABCD (AB//CD), AB < CD. Đường cao BH chia cạnh CD thành 2 đoạn DH = 16cm, HC = 9cm. Biết BD vuông góc BC.a)Tính đường chéo AC và BD của hình thangb)Tính diện tích hình thangc)Tính chu vi hình thang
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Tính diện tích tứ giác DENM.
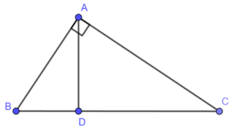
Cho tam giác ABC vuông tại A, đường cao AH, phân giác góc B cắt AH tại I và cắt AC tại D. C/m:
a, tam giác HBA ddoognf dạng tam giác ABC
b, IH.DC=IA.AD
c, Giả sử phân giác AG của góc BAC chia cạnh huyền BC thành 2 đoạn có độ dài là 1 cm và 3cm ( G thuộc BC). TÍnh tỉ số BH trên HC
Mọi ng giúp mk nhé
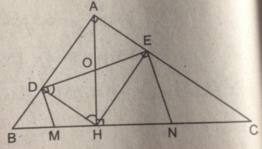
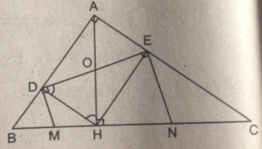
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.Gọi D và E là hình chiếu của H trên AB và AC.Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.
Đọc tiếp
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.
1/Cho hình thang ABCD, đáy ADBC, các cạnh bên AB và CD kéo dài cắt nhau tại M.Tính đoạn CD, nếu frac{AM}{AB+BM}frac{1}{4}, 2CM+5DM120m2/Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng đó có độ dài 9cm và 16cm. Tìm độ dài các cạnh của tam giác vuông đó.3/ Cho 2 tam giác đồng dạng có tỉ số chu vi là 13/15. Hiệu hai cạnh tương ứng là 4m. Tính hai cạnh đó.Giúp mình với, mình cần gấp. Mấy bạn đưa ra gợi ý cũm đc
Đọc tiếp
1/Cho hình thang ABCD, đáy AD<BC, các cạnh bên AB và CD kéo dài cắt nhau tại M.
Tính đoạn CD, nếu \(\frac{AM}{AB+BM}=\frac{1}{4}\), 2CM+5DM=120m
2/Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng đó có độ dài 9cm và 16cm. Tìm độ dài các cạnh của tam giác vuông đó.
3/ Cho 2 tam giác đồng dạng có tỉ số chu vi là 13/15. Hiệu hai cạnh tương ứng là 4m. Tính hai cạnh đó.
Giúp mình với, mình cần gấp. Mấy bạn đưa ra gợi ý cũm đc
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm; Tính độ dài các cạnh của tam giác vuông.
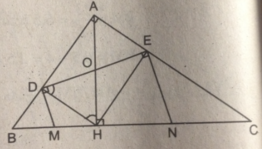
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Tính độ dài DE
Cho hình chữ nhật ABCD có AB = 12cm, BC = 9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD a) C/m: tam giác AHB đồng dạng tam giác BCD b) Tính độ dài đoạn AH c) Tính diện tích tam giác AHB d) AH cắt đường thẳng BC tại K, cắt DC tại I. C/m: AH2 = HI.HK]







