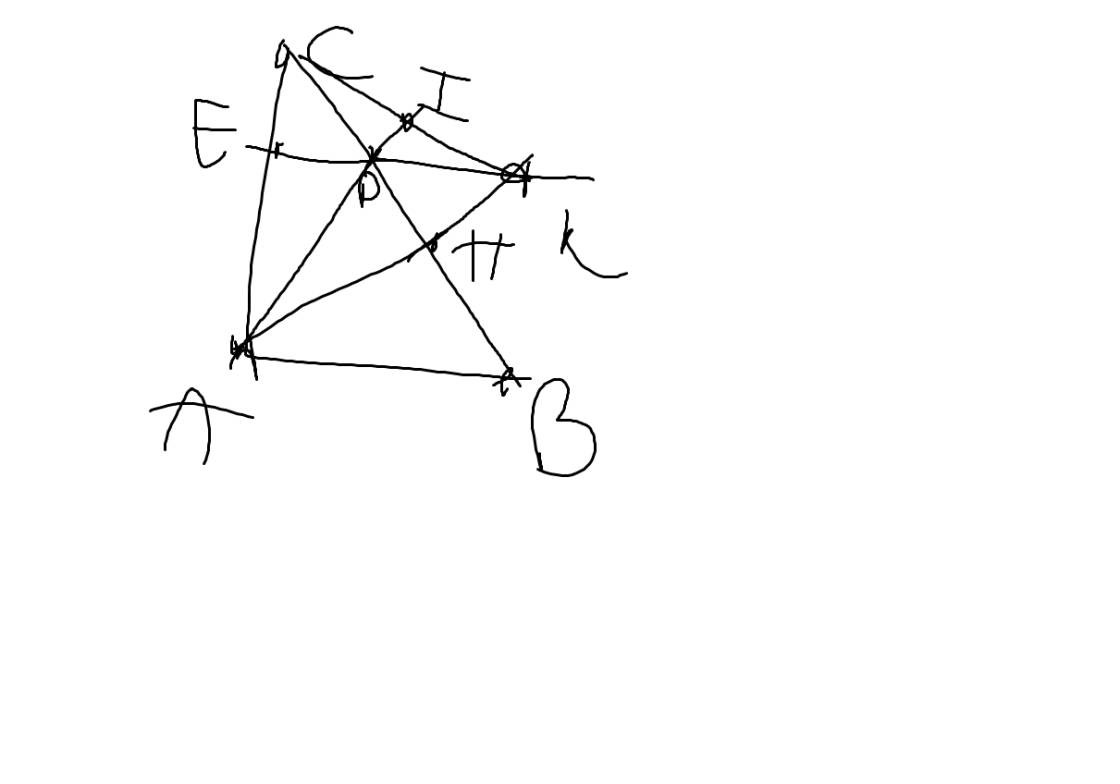
cho ΔABC vuông tại A (AB<AC) , đg cao AH . Trên cạnh AC , lấy điểm E sao cho AH = AE . Qua E kẻ đg vuông góc với AC , cắt cạnh BC tại D
CM : a) ΔAHD = ΔAED và AD là tia phân giác của góc HAC
b) tia ED cắt tia AH tại K . CM Δ KCD cân
c)so sánh BK và AK
d) I là trung điểm của KC . CM A,D,I thẳng hành (VẼ HÌNH)
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
Do đó: ΔAHD=ΔAED
=>\(\widehat{HAD}=\widehat{EAD}\)
=>AD là phân giác của góc HAC
b: Ta có: ΔAHD=ΔAED
=>DH=DE
Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó; ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
d: Ta có: AH+HK=AK
AE+EC=AC
mà AH=AE và HK=EC
nên AK=AC
=>A nằm trên đường trung trực của KC(1)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(2)
Ta có: IC=IK
=>I nằm trên đường trung trực của KC(3)
từ (1),(2), (3) suy ra A,D,I thẳng hàng
a) Để chứng minh tam giác ABH = tam giác ACH, ta cần chứng minh AB = AC và góc BAH = góc CAH.
Vì tam giác ABH là tam giác cân tại A, nên AB = AH.
Vì H là trung điểm của BC, nên BH = HC.
Vì H là trung điểm của BC, nên AH là tia phân giác của góc BAC.
Do đó, ta có AB = AH, BH = HC và AH là tia phân giác của góc BAC. Từ đây, theo nguyên lý đẳng thức tam giác, ta có tam giác ABH = tam giác ACH.
b) Để chứng minh tam giác ADH là tam giác cân, ta cần chứng minh AD = DH.
Vì D là giao điểm của đường thẳng đi qua H song song với AC và AB, nên theo tính chất của đường song song, ta có góc AHD = góc BAC.
Vì AH là tia phân giác của góc BAC, nên góc BAH = góc CAH. Kết hợp với góc AHD = góc BAC, ta có góc AHD = góc BAH = góc CAH.
Vậy, tam giác ADH là tam giác cân, và do đó, AD = DH.
cho ΔABC vuông tại A (AB<AC) , đg cao AH . Trên cạnh AC , lấy điểm E sao cho AH = AE . Qua E kẻ đg vuông góc với AC , cắt cạnh BC tại D
CM : a) ΔAHD = ΔAED và AD là tia phân giác của góc HAC
Copyb) tia ED cắt tia AH tại K . CM Δ KCD cân c)so sánh BK và AK
Assistant
Poea) Để chứng minh ΔAHD = ΔAED, ta cần chứng minh AH = AE và góc AHD = góc AED.
Vì AH = AE (theo giả thiết), ta đã có AH = AE.
Ta biết rằng AH là đường cao của tam giác ABC, do đó góc AHB = 90 độ.
Vì góc AED là góc giữa đường thẳng ED và AC (do đường thẳng ED là đường vuông góc với AC), và góc AHD là góc giữa đường thẳng HD và AC (do đường thẳng HD là đường vuông góc với AC), nên để chứng minh góc AHD = góc AED, ta cần chứng minh góc AHB = góc AED.
Tuy nhiên, vì góc AHB = 90 độ và góc AED là góc giữa đường thẳng ED và AC, nên góc AHB = góc AED.
Vì AH = AE và góc AHB = góc AED, theo nguyên lý đẳng thức tam giác, ta kết luận ΔAHD = ΔAED.
Để chứng minh AD là tia phân giác của góc HAC, ta cần chứng minh góc CAD = góc BAD.
Vì ΔABC là tam giác vuông tại A, nên góc BAD = 90 độ.
Vì AH = AE và ΔAHD = ΔAED (đã được chứng minh ở trên), nên góc AHD = góc AED.
Kết hợp với góc BAD = 90 độ, ta có góc AHD = góc BAD = góc AED.
Do đó, AD là tia phân giác của góc HAC.
b) Để chứng minh ΔKCD là tam giác cân, ta cần chứng minh góc KCD = góc KDC.
Vì tia ED là đường vuông góc với AC và tia AH cắt tia ED tại K, nên góc KCD = góc KAC.
Vì AD là tia phân giác của góc HAC, nên góc KAC = góc KAD.
Vì ΔAHD = ΔAED (đã được chứng minh ở câu a), nên góc KAD = góc KED.
Tuy nhiên, vì tia AH = tia AE và tia ED là đường vuông góc với AC, nên góc KED = góc KAE.
Kết hợp góc KAC = góc KAD và góc KAD = góc KED = góc KAE, ta có góc KCD = góc KAC = góc KAE.
Vậy, ΔKCD là tam giác cân.
c) Bằng cách so sánh ΔBAK và ΔBAK, ta có:
Góc BAK = góc BAK (cùng là góc giữa đường thẳng AK và AC)
Góc AKB = góc AKC (cùng là góc giữa đường thẳng KC và AC, do tia AD là tia phân giác của góc HAC)
AK = AK (cùng là cạnh chung)
Do đó, theo nguyên lý đẳng thức tam giác, ΔBAK = ΔBAK.
Vậy, BK = AK.















