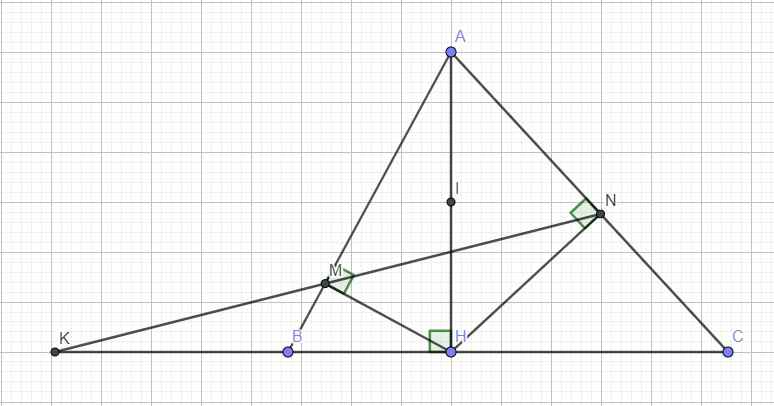
Gọi I là trung điểm AH
M và N đều nhìn AH dưới 1 góc vuông \(\Rightarrow\) tứ giác AMHN nội tiếp đường tròn (I) đường kính AH
Mặt khác \(IH\perp KH\Rightarrow KH\) là tiếp tuyến của (I)
Theo tính chất phương tích: \(KH^2=KM.KN\)
Lại có: \(\widehat{AHN}=\widehat{ACB}\) (cùng phụ \(\widehat{HAN}\))
\(\widehat{AHN}=\widehat{AMN}\) (cùng chắn cung AN của đường tròn (I))
\(\widehat{AMN}=\widehat{KMB}\) (đối đỉnh)
\(\Rightarrow\widehat{KMB}=\widehat{ACB}\)
Xét hai tam giác KMB và KCN có:
\(\left\{{}\begin{matrix}\widehat{BKM}\text{ chung}\\\widehat{KMB}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta KMB\sim\Delta KCN\left(g.g\right)\)
\(\Rightarrow\dfrac{KB}{KN}=\dfrac{KM}{KC}\Rightarrow KM.KN=KB.KC\)
\(\Rightarrow KH^2=KB.KC\)