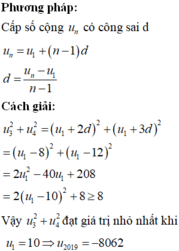Các câu hỏi tương tự
Cho cấp số cộng
u
n
có công sai d -4 và
u
3
2
+
u
4
2
đạt giá trị nhỏ nhất. Tìm
u
2018
là số hạng thứ 2018 của cấp số cộng đó. A.
u
2018
−
8062
B.
u
2018...
Đọc tiếp
Cho cấp số cộng u n có công sai d = -4 và u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tìm u 2018 là số hạng thứ 2018 của cấp số cộng đó.
A. u 2018 = − 8062
B. u 2018 = − 8060
C. u 2018 = − 8058
D. u 2018 = − 8054
Cho ba số
2017
+
log
2
a
,
2018
+
log
3
a
và
2019
+
l
o
g
4
a
theo thứ tự lập thành một cấp số cộng. Công sai của cấp số cộng này bằng A. 1. B. 12. C. 9. D. 20.
Đọc tiếp
Cho ba số 2017 + log 2 a , 2018 + log 3 a và 2019 + l o g 4 a theo thứ tự lập thành một cấp số cộng. Công sai của cấp số cộng này bằng
A. 1.
B. 12.
C. 9.
D. 20.
Cho ba số
2017
+
log
2
a
,
2018
+
log
3
a
và
2019
+
log
4
a
theo thứ tự lập thành một cấp số cộng. Công sai của cấp số cộng này bằng A. 1. B. 12. C. 9. D. 20.
Đọc tiếp
Cho ba số 2017 + log 2 a , 2018 + log 3 a và 2019 + log 4 a theo thứ tự lập thành một cấp số cộng. Công sai của cấp số cộng này bằng
A. 1.
B. 12.
C. 9.
D. 20.
Cho cấp số cộng
u
n
có công sai
d
−
3
và
u
2
2
+
u
3
2
+
u
4
2
đạt giá trị nhỏ nhất. Tính tổng
S
100
của 100 số hạng đầu tiên của cấp số cộng đó. A.
S...
Đọc tiếp
Cho cấp số cộng u n có công sai d = − 3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng S 100 của 100 số hạng đầu tiên của cấp số cộng đó.
A. S 100 = − 14400.
B. S 100 = − 14250.
C. S 100 = − 15480.
D. S 100 = − 14650.
Cho cấp số cộng
u
n
có công sai d -3 và
u
2
2
+
u
3
2
+
u
4
2
đạt giá trị nhỏ nhất. Tính tổng
S
100
của 100 số hạng đầu tiên của cấp số cộng đó. A.
S
100
-14650 B....
Đọc tiếp
Cho cấp số cộng u n có công sai d = -3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng S 100 của 100 số hạng đầu tiên của cấp số cộng đó.
A. S 100 = -14650
B. S 100 = -14400
C. S 100 = -14250
D. S 100 = -15450
Cho cấp số cộng
u
n
có công sai d -3 và
u
2
2
+
u
3
2
+
u
4
2
đạt giá trị nhỏ nhất. Tính tổng
s
100
của 100 số hạng đầu tiên của cấp số cộng đó. A.
s
100
-
14550
B.
s
100...
Đọc tiếp
Cho cấp số cộng u n có công sai d = -3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng s 100 của 100 số hạng đầu tiên của cấp số cộng đó.
A. s 100 = - 14550
B. s 100 = - 14400
C. s 100 = - 14250
D. s 100 = - 15450
Cho cấp số cộng
u
n
có công sai
d
−
3
và
u
2
2
+
u
3
2
+
u
4
2
đạt giá trị nhỏ nhất. Tính tổng
S
100
của 100 số hạng đầu tiên của cấp số cộng đó. A.
S...
Đọc tiếp
Cho cấp số cộng u n có công sai d = − 3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng S 100 của 100 số hạng đầu tiên của cấp số cộng đó.
A. S 100 = − 14650
B. S 100 = − 14400
C. S 100 = − 15450
D. S 100 = − 14250
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
thỏa mãn a,b,c,dÎR; a 0 và
d
2019
8
a
+
4...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d thỏa mãn a,b,c,dÎR; a > 0 và d > 2019 8 a + 4 b + 2 x + d - 2019 < 0 . Số cực trị của hàm số y = | f ( x ) - 2019 | bằng
A. 3
B. 2
C. 1
D. 5
Cho m, n là các số nguyên dương khác 1. Gọi P là tích các nghiệm của phương trình
2018
log
m
x
log
n
x
2017
log
m
x...
Đọc tiếp
Cho m, n là các số nguyên dương khác 1. Gọi P là tích các nghiệm của phương trình 2018 log m x log n x = 2017 log m x + 2018 log n x + 2019 . P nguyên và đạt giá trị nhỏ nhất khi:
A. m . n = 2 2020 .
B. m . n = 2 2017 .
C. m . n = 2 2019 .
D. m . n = 2 2018 .