Các câu hỏi tương tự
Cho số thực a dương khác 1. Biết rằng bất kỳ đường thẳng nào song song với trục Ox mà cắt đường thẳng
y
4
x
,
y
a
x
, trục tung lần lượt tại M, N và A thì AN 2AM. Giá trị của a bằng A.
1
2
B.
1
3
C.
2
2
D.
1...
Đọc tiếp
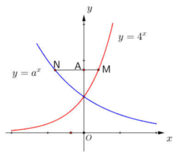
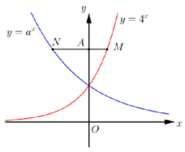
Cho số thực a dương khác 1. Biết rằng bất kỳ đường thẳng nào song song với trục Ox mà cắt đường thẳng y = 4 x , y = a x , trục tung lần lượt tại M, N và A thì AN = 2AM. Giá trị của a bằng
A. 1 2
B. 1 3
C. 2 2
D. 1 4
Cho các số thực dương a, b khác 1. Biết rằng bất kì đường thẳng nào song song với Ox mà cắt các đường
y
a
x
,
y
b
x
,
trục tung lần lượt tại M, N và A thì AN 2AM (hình vẽ bên). Mệnh đề nào sau đây đúng? A.
a
2
b...
Đọc tiếp
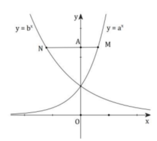
Cho các số thực dương a, b khác 1. Biết rằng bất kì đường thẳng nào song song với Ox mà cắt các đường y = a x , y = b x , trục tung lần lượt tại M, N và A thì AN = 2AM (hình vẽ bên). Mệnh đề nào sau đây đúng?
A. a 2 = b .
B. b = 2a
C. ab 2 = 1 .
D. a = b 2
Cho a, b là các số thực dương khác 1. Các hàm số
y
a
x
và
y
b
x
có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số
y
a
x
,
y
b
x
, trục tung lần lượt tại M, N, A đều thỏa mãn AN 2AM. Mệnh đề nào sau đây đúng? A. b 2a B.
a...
Đọc tiếp
Cho a, b là các số thực dương khác 1. Các hàm số y = a x và y = b x có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số y = a x , y = b x , trục tung lần lượt tại M, N, A đều thỏa mãn AN = 2AM. Mệnh đề nào sau đây đúng?
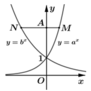
A. b = 2a
B. a 2 = b
C. a b = 1 2
D. a b 2 = 1
Cho các số thực dương a, b khác 1. Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt đồ thị các hàm số
y
a
x
,
y
b
x
trục tung lần lượt tại M, N, a thì
A
N
3
A
M
. Mệnh đề nào dưới đây đúng? A.
a
b
3
1
B.
a...
Đọc tiếp
Cho các số thực dương a, b khác 1. Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt đồ thị các hàm số y = a x , y = b x trục tung lần lượt tại M, N, a thì A N = 3 A M . Mệnh đề nào dưới đây đúng?
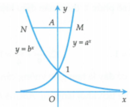
A. a b 3 = 1
B. a 3 b = 1
C. a = 3b
D. a = b 3
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị
y
log
a
x
,
y
log
b
x
và trục hoành lần lượt tại A, B và H ta đều có
2
H
A
3
H
B
(hình vẽ bên). Khẳng định nào sau đây đúng? A.
a
2...
Đọc tiếp
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị y = log a x , y = log b x và trục hoành lần lượt tại A, B và H ta đều có 2 H A = 3 H B (hình vẽ bên). Khẳng định nào sau đây đúng?
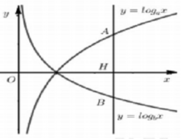
A. a 2 b 3 = 1
B. 3 a = 2 b
C. 2 a = 3 b
D. a 3 b 2 = 1
Cho các số thực dương a, b khác 1. Biết rằng đường thẳng y2 cắt đồ thị của các hàm số
y
a
x
,
y
b
x
và trục tung lần lượt tại A, B và C sao cho C nằm giữa A và B và AC2BC. Khẳng định nào dưới đây đúng A. b
a
2
B. b2a C. b
a
-
2
D. b...
Đọc tiếp
Cho các số thực dương a, b khác 1. Biết rằng đường thẳng y=2 cắt đồ thị của các hàm số y = a x , y = b x và trục tung lần lượt tại A, B và C sao cho C nằm giữa A và B và AC=2BC. Khẳng định nào dưới đây đúng
A. b= a 2
B. b=2a
C. b= a - 2
D. b= a 2
Cho hai số thực dương a, b khác 1 và đồ thị của các hàm số
y
log
a
x
,
y
log
b
x
như hình vẽ bên. Gọi d là đường thẳng song song với trục Oy và cắt trục hoành tại điểm A có hoành độ xk(k1) Gọi S1 là diện tích hình phẳng giới hạn bởi
y
log
a
x
,
d
và trục hoành; S2 là...
Đọc tiếp
Cho hai số thực dương a, b khác 1 và đồ thị của các hàm số y = log a x , y = log b x như hình vẽ bên. Gọi d là đường thẳng song song với trục Oy và cắt trục hoành tại điểm A có hoành độ x=k(k>1) Gọi S1 là diện tích hình phẳng giới hạn bởi y = log a x , d và trục hoành; S2 là diện tích hình phẳng giới hạn bởi y = log b x , d và trục hoành. Biết S1 = 4S2. Mệnh đề nào sau đây đúng ?
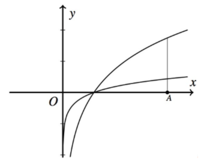
A. b = a 4
B. a = b 4
C. b = a 4 ln 2
D. a = b 4 ln 2
Cho hàm số
y
2
x
+
1
x
−
1
có đồ thị là (H) và đường thẳng d có hệ số góc m và đi qua điểm
A
−
2
;
2
. Giả sử d cắt (H) tại hai điểm phân biệt M, N. Qua M kẻ các đường thẳng lần lượt song song với các trục tọa độ, qua N kẻ các đường thẳng lần lượt song song với các trục...
Đọc tiếp
Cho hàm số y = 2 x + 1 x − 1 có đồ thị là (H) và đường thẳng d có hệ số góc m và đi qua điểm A − 2 ; 2 . Giả sử d cắt (H) tại hai điểm phân biệt M, N. Qua M kẻ các đường thẳng lần lượt song song với các trục tọa độ, qua N kẻ các đường thẳng lần lượt song song với các trục tọa độ. Tìm số các giá trị thực của tham số m sao cho bốn đường thẳng đó tạo thành một hình vuông.
A. 0
B. 1
C. 2
D. 3
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số
y
log
a
x
,
y
log
a
x
,
y
log
a
3
x
, với (x0;a1). Giá trị của a là A...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với (x>0;a>1). Giá trị của a là
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6