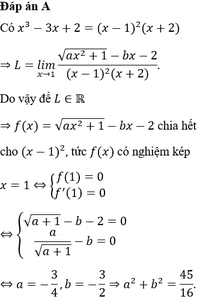Các câu hỏi tương tự
Cho 2 số thực x;y thỏa mãn
x
,
y
≥
1
và
log
3
x
+
1
y
+
1
y
+
1
9...
Đọc tiếp
Cho 2 số thực x;y thỏa mãn x , y ≥ 1 và log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 Biết giá trị nhỏ nhất của biểu thức P = x 3 + y 3 − 57 x + y là một số thực có dạng a + b 7 , a , b ∈ ℤ . Tính giá trị của a+b
A. -28
B. -29
C. -30
D. -31
Cho các số thực dương x, y thỏa mãn
log
x
+
y
x
2
+
y
2
≤
1
.Giá trị lớn nhất của biểu thức A
48
(
x
+
y
)
3
-
156
(
x
+
y...
Đọc tiếp
Cho các số thực dương x, y thỏa mãn log x + y x 2 + y 2 ≤ 1 .Giá trị lớn nhất của biểu thức A= 48 ( x + y ) 3 - 156 ( x + y ) 2 + 133 ( x + y ) + 4 là
A. 29.
B. 1369/36.
C. 30.
D. 505/36
Cho biết
l
i
m
x
→
1
2
a
x
2
+
1
-
b
x
-
2
4...
Đọc tiếp
Cho biết l i m x → 1 2 a x 2 + 1 - b x - 2 4 x 3 - 3 x + 1 ( a , b ∈ R ) có kết quả là một số thực. Giá trị biểu thức a+b bằng
A. = -6
B. = -4
C. = -5
D. = -9
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A(a;0;0),B(0;b;0),C(0;0;c) với a,b,c là các số thực thay đổi thoả mãn
1
a
-
2
b
+
2
c
1
. Biết rằng mặt cầu (S):
(
x
-
2
)
2
+
y
2
+
(
z
-
4...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A(a;0;0),B(0;b;0),C(0;0;c) với a,b,c là các số thực thay đổi thoả mãn 1 a - 2 b + 2 c = 1 . Biết rằng mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z - 4 ) 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a+b+c bằng
A. 5.
B. 1.
C. 2.
D. 4.
Cho a, b là các số thực và hàm số
f
x
x
−
a
−
1
x
2
−
4...
Đọc tiếp
Cho a, b là các số thực và hàm số f x = x − a − 1 x 2 − 4 k h i x ≠ 2 2 x − b k h i x = 2 liên tục tại x = 2. Tính giá trị của biểu thức T=a+b.
A. T = 31 8
B. T = 5
C. T = 3
D. T = 39 8
Cho
a
,
b
là các số thực và
f
x
a
ln
2017
x
2
+
1
+
x
+
b
x
sin
2018
x
+
2.
Biết
f
5...
Đọc tiếp
Cho a , b là các số thực và f x = a ln 2017 x 2 + 1 + x + b x sin 2018 x + 2. Biết f 5 log c 6 = 6 , tính giá trị của biểu thức P = f − 6 log c 5 với 0 < c ≠ 1
A. P = − 2
B. P = 6
C. P = 4
D. P = 2
Cho hàm số
f
x
a
x
+
b
c
x
+
d
với
a
,
b
,
c
,
d
∈
R
có đồ thị hàm số yf(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số yf(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng. A. 2 B. 5 C. 4...
Đọc tiếp
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Biết rằng a, b là hai giá trị thực để hàm số
f
x
x
+
2
−
a
x
x
−
2
,...
Đọc tiếp
Biết rằng a, b là hai giá trị thực để hàm số f x = x + 2 − a x x − 2 , x > 2 a x + b , x ≤ 2 liên tục tại x = 2 . Tính giá trị biểu thức P = a + 4 b
A. -10
B. 6
C. 2
D. -6
Cho hai số thực không âm x,y ≤ 1. Biết
P
l
n
(
1
+
x
2
)
(
1
+
y
2
)
+
8
17
(
x
+
y
)
2
có giá trị nhỏ nhất là
-
a
b
+
2
ln
c...
Đọc tiếp
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405