a: Xét tứ giác ADHP có
AD//HP
AP//HD
Do đó: ADHP là hình bình hành
Hình bình hành ADHP có \(\widehat{DAP}=90^0\)
nên ADHP là hình chữ nhật
=>AH=DP
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>ΔMAC cân tại M
Phần Hình Học :
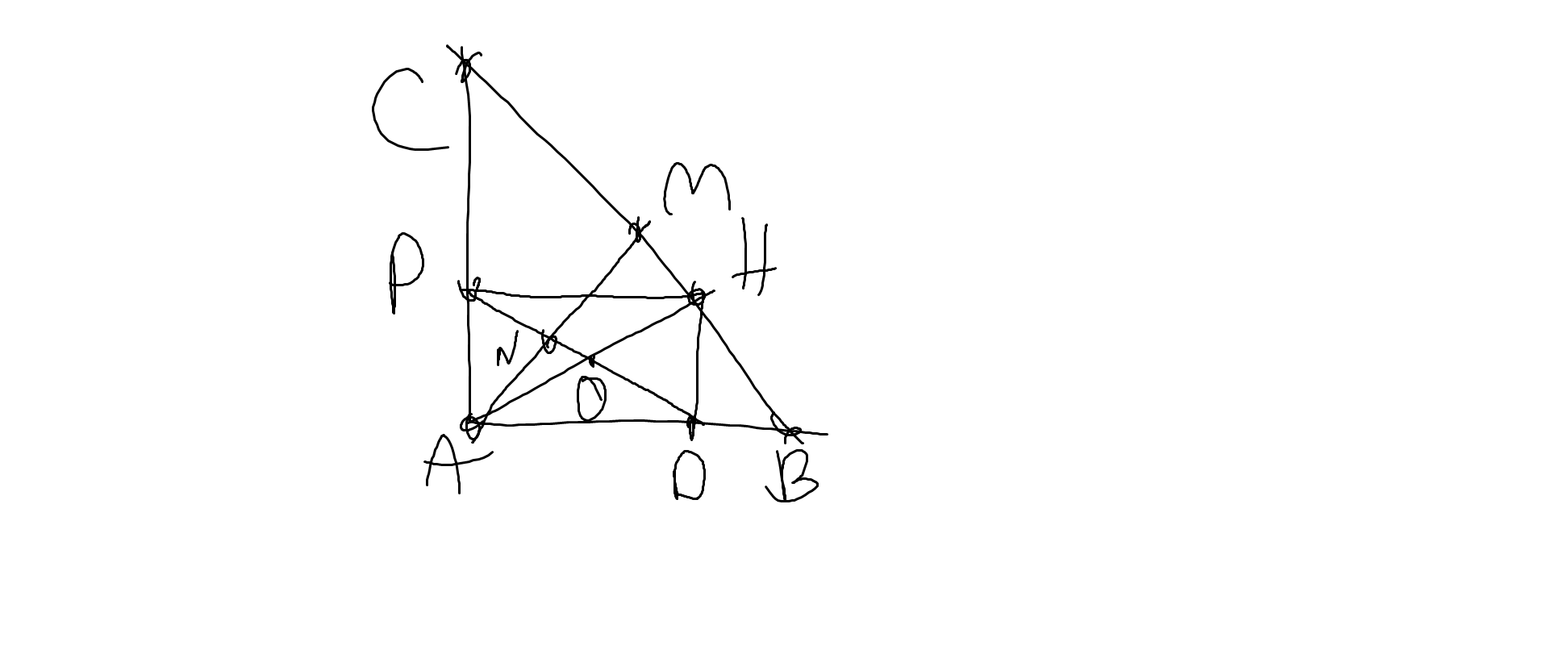
Bài 1 : Cho Δ ABC vuông tại A có AH là đường cao, đường trung tuyến AM. Qua H kẻ HD // AC ( D ∈ AC). Đoạn DP cắt AH, AM lần lượt tại O và N.
a, Chứng minh AH = DP.
b, ΔMAC là tam giác gì ?
c, Chứng minh ΔAPN là tam giác vuông.
Bài 2. Cho ΔABC vuông tại A có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, Chứng minh ABCD là hình chữ nhật.
b, Lấy điểm E sao cho B là trung điểm của AE. Chứng minh BEDC là hình bình hành.
c, EM cắt BD tại K. Chứng minh EK = 2KM.
tam giác ABC vuông tại A có, đường cao AH, đường trung tuyến AM. Từ H kẻ HD,HE lần lượt vuông góc với AB,AC. a) Chứng minh ADHE là hình chữ nhật. b) Chứng minh AM Vuông góc DE. c) Gọi O là giao điểm của AH và DE. Qua A kẻ tia Ax vuông góc với đường thẳng MO tại P cắt tia CB tại N. Chứng minh: 3 điểm N, D, E thẳng hàng HÉP MY
Cho tam giác ABC vuông tại A có AH là đường cao, AM là đường trung tuyến. Qua H kẻ đường thẳng song song với AB và AC, lần lượt cắt AC ở E và AB ở D. DE cắt AH ở O và AM ở I.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Tính \(\widehat{AIE}\)?
Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM. Kẻ HE và HD lần lượt vuông góc với AB,AC. Kẻ MK vuông góc AB. N là giao điểm của AM và HE
C/m:
a) AM vuông góc DE
b) BN//DE
c) MK,BN,AH đồng quy
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là chân các đường cao bhaj từ H xuống AB và AC.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Cho AB =10cm,BH=6cm. Tính DE.
c) Qua A kẻ đường vuông góc với DE cắt BC tại M. C/m AM là đường trung tuyến của tam giác ABC .
Câu 1: Cho tam giác ABC vuông tại A, đường cao AH, D và E là 2 đường vuông góc kẻ từ H đến AB và AC.
A) Chứng minh AH=DE
B) I là trung điểm HB, K là trung điểm HC. Chứng minh DI song song với EK
Câu 2: Cho tam giác ABC vuông góc tại A, đường cao AH, trung tuyến AM.
A) Chứng minh góc HAB = góc MAC
B) Vẽ HD vuông góc với AB, HE vuông góc với AC. Chứng minh AM vuông góc với DE.
cho tam giác ABC cân tại A đường cao ah gọi E,F lần lượt là chân đường vuông góc hạ từ H xuống AB,AC a) c/m EF=AH b) Kẻ trung tuyến AM của tam giác ABC C/m AM vuông góc EF
Cho tam giác ABC, trung tuyến AM, đường cao AH. Kẻ HE và HD lần lượt vuông góc với AB,AC. Kẻ MK vuông góc với AB. Gọi N là giao điểm của AM và HD. Cm:
a) AM vuông góc với DE
b) BN//DE
c) MK, BN,AH đồng quy
Cho tam giác ABC vuông tại A (AB < AC) kẻ đường cao AH và trung tuyến
AM (H, M thuộc BC). Qua A kẻ đường thẳng vuông góc với AM và cắt đường thẳng
BC tại D.
a) Chứng minh AB là phân giác của góc DAH;
b) Chứng minh BH.CD = CH.BD.
Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM. Kẻ HE và HD lần lượt vuông góc với AB,AC. Kẻ MK vuông góc AB. N là giao điểm của AM và HE
C/m:
a) AM vuông góc DE
b) BN//DE
c) MK,BN,AH đồng quy
GIÚP TỚ VS !!! TỚ ĐANG CẦN LẮM LUÔN!!!!
