Question

Cho  ABC nhọn, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn

 ( O ), đường kính AH. Gọi M là trung điểm BC.

  a/ Chứng minh EM là tiếp tuyến của đường tròn ( O ).

Answer 1

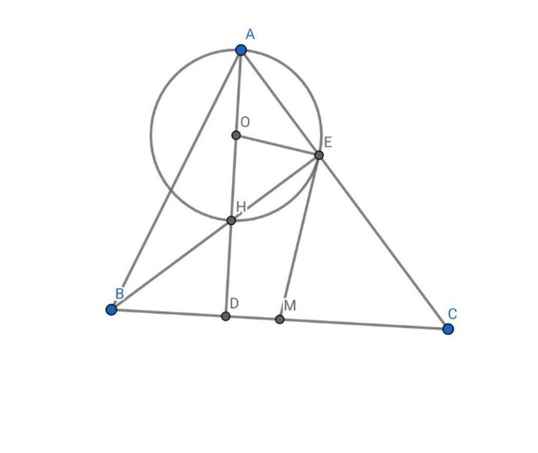
Có \(\widehat{AEH}=90^o\)

=> ΔAEH vuông tại E có ED là đường trug tuyến

\(\Rightarrow ED=\dfrac{AH}{2};E\in\left(O\right)\)

=> EO là bán kính (O)

lại có : OE=OH=R

=> \(\widehat{OEH}=\widehat{BHD};vì\widehat{OHE}=\widehat{BHD}\left(dđ\right)\)

=> ΔOEH cân tại O

cm tương tự có ΔEMB cân tại M

=> \(\widehat{MEB}=\widehat{MBH}\)

\(\widehat{OEM}=\widehat{OEH}+\widehat{EHM}\)

\(=\widehat{DBH}+\widehat{BHD}=90^o\)

từ đó suy ra : OE ⊥ EM

<=>EM là tiếp tuyến của đường tròn ( O ).

Answer 2

Giúp zới =(((

Answer 3

Hình: