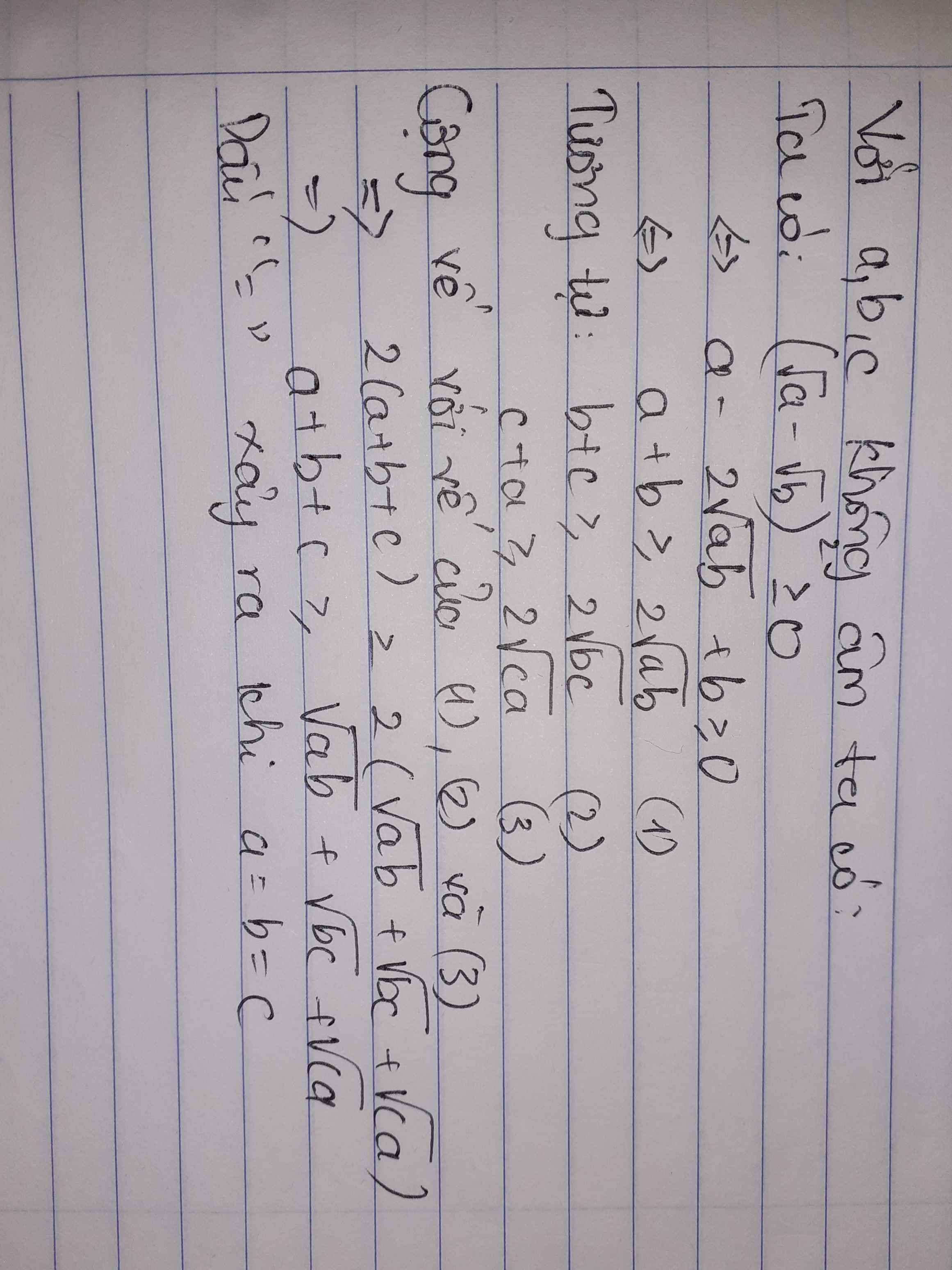Điều phải chứng minh tương đương với
\(2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\\ \Leftrightarrow\left(a+b-2\sqrt{ab}\right)+\left(b+c-2\sqrt{bc}\right)+\left(c+a-2\sqrt{ca}\right)\ge0\\ \Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)
(luôn đúng với mọi a,b,c không âm)
Dấu = xảy ra khi a=b=c >=0
Ta có: \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\)
\(\Leftrightarrow\left(a-2\sqrt{ab}+b\right)+\left(b-2\sqrt{bc}+c\right)+\left(a-2\sqrt{ac}+c\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{a}-\sqrt{c}\right)^2\ge0\)(luôn đúng)