Cho △ ABC có AB=AC .M và N lần lượt là trung điểm cạnh AB và cạnh AC.Trên cạnh BC lấy điểm D và E sao cho BD=DE=EC
a)Chứng minh △ MBE= △ NCD
b)Gọi I là giao điểm ME và ND.Chứng minh △ IDE cân
c)Chứng minh AI vuông góc với BC
d)Trên tia AC lấy điểm F sao cho C là trung điểm của AF.Chứng minh E,M,F thẳng hàng
CẦN CẢ HÌNH VẼ TAM GIÁC
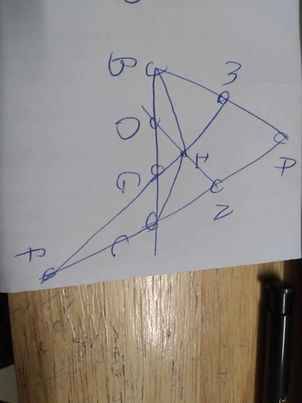
a:
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Ta có: BE=BD+DE
CD=CE+ED
mà BD=CE
nên BE=CD
Xét ΔMBE và ΔNCD có
MB=NC
\(\widehat{MBE}=\widehat{NCD}\)
BE=CD
Do đó; ΔMBE=ΔNCD
b: Ta có: ΔMBE=ΔNCD
=>\(\widehat{MEB}=\widehat{NDC}\)
=>\(\widehat{IDE}=\widehat{IED}\)
=>ΔIED cân tại I
c: Ta có: ΔMBE=ΔNCE
=>ME=ND
Ta có: ME=MI+IE
ND=NI+ID
mà IE=ID và ME=ND
nên MI=NI
Xét ΔIMB và ΔINC có
IM=IN
\(\widehat{IMB}=\widehat{INC}\)(ΔMBE=ΔNCD)
MB=NC
Do đó: ΔIMB=ΔINC
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI\(\perp\)BC
d: \(\dfrac{BE}{BC}=\dfrac{2BD}{3BD}=\dfrac{2}{3}\)
Xét ΔBAF có
BC là đường trung tuyến
\(BE=\dfrac{2}{3}BC\)
Do đó: E là trọng tâm của ΔBAF
Xét ΔBAF có
E là trọng tâm
M là trung điểm của AB
Do đó: F,E,M thẳng hàng












