Các câu hỏi tương tự
Cho điểm
A
1
;
0
;
0
và mặt phẳng
P
:
y
+
z
-
3
0
. Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
Đọc tiếp
Cho điểm A 1 ; 0 ; 0 và mặt phẳng P : y + z - 3 = 0 . Điểm M di động trên (P), xác định độ dài ngắn nhất của AM.
![]()
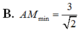
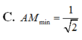
![]()
Cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
+
1
2
4...
Đọc tiếp
Cho mặt cầu S : x - 1 2 + y - 2 2 + z + 1 2 = 4 và mặt phẳng P : 2 x + 2 y - z + 2 = 0 . Điểm M di động trên (S), N di động trên (P). Tìm độ dài ngắn nhất của đoạn MN
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm A(1;2;-3) mặt phẳng (P): 2x+2y-z+90 và đường thẳng
∆
:
x
+
1
3
y
4
z
+
2
-
4
Đường thẳng d đi qua A, song song với
∆
và cắt tại B. Điểm M di động trên (P) sao c...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;2;-3) mặt phẳng (P): 2x+2y-z+9=0 và đường thẳng ∆ : x + 1 3 = y 4 = z + 2 - 4 Đường thẳng d đi qua A, song song với ∆ và cắt tại B. Điểm M di động trên (P) sao cho tam giác AMB luôn vuông tại M. Độ dài đoạn MB có giá trị lớn nhất bằng
![]()
![]()
![]()
![]()
Cho
A
0
;
1
;
-
2
,
B
-
2
;
3
;
2
và
C
1
;
-
2
;
-
3
. Điểm M...
Đọc tiếp
Cho A 0 ; 1 ; - 2 , B - 2 ; 3 ; 2 và C 1 ; - 2 ; - 3 . Điểm M di động trên đường thẳng AB. Khi đó độ dài CM ngắn nhất bằng:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng
(
α
)
:
2
x
+
2
y
+
z
-
12
0
Điểm M di động trên mặt phẳng
(
α
)
sao cho MA, MB luôn tạo với ...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng ( α ) : 2 x + 2 y + z - 12 = 0 Điểm M di động trên mặt phẳng ( α ) sao cho MA, MB luôn tạo với ( α ) các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn ( ω ) cố định. Hoành độ của tâm đường tròn ( ω ) bằng
A. 9 2
B. 2
C. 10
D. -4
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 0 có duy nhất một nghiệm. A. m
≤
2015, m
≥
2019. B. 2015 m 2019. C. m 2015, m 2019. D. m 2015, m 2019.
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
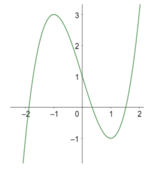
A. m ≤ 2015, m ≥ 2019.
B. 2015 < m < 2019.
C. m = 2015, m = 2019.
D. m < 2015, m > 2019.
Xác định giá trị của tham số m để phương trình
1
3
x
3
-
1
2
mx
2
-
5
0
có nghiệm duy nhấtA. m
-
30...
Đọc tiếp
Xác định giá trị của tham số m để phương trình
1 3 x 3 - 1 2 mx 2 - 5 = 0
có nghiệm duy nhất
A. m < - 30 3 B. 0 < m < 1
C. m < 0 D. m > - 30 3
Trong không gian Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) di động trên các trục Ox, Oy, Oz sao cho 2a+b-c-60 và hai điểm M(2;-3;5). Xét các mặt cầu (S) ngoại tiếp tứ diện OABC có tâm I. Khi
2
I
M
→
+
I
N
→
đạt giá trị nhỏ nhất thì mặt cầu (S)...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) di động trên các trục Ox, Oy, Oz sao cho 2a+b-c-6=0 và hai điểm M(2;-3;5). Xét các mặt cầu (S) ngoại tiếp tứ diện OABC có tâm I. Khi 2 I M → + I N → đạt giá trị nhỏ nhất thì mặt cầu (S) có diện tích bằng
A. 14 π .
B. 64 π .
C. 56 π .
D. 16 π .
Trong không gian Oxyz, cho điểm A(1;0;2), B(−2;0;5), C(0;−1;7). Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A lấy một điểm S. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết khi S di động trên d (S ≠ A) thì đường thẳng HK luôn đi qua một điểm cố định D. Tính độ dài đoạn thẳng AD. A. AD 3
3
B. AD
6
2
C. AD
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;2), B(−2;0;5), C(0;−1;7). Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A lấy một điểm S. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết khi S di động trên d (S ≠ A) thì đường thẳng HK luôn đi qua một điểm cố định D. Tính độ dài đoạn thẳng AD.
A. AD = 3 3
B. AD = 6 2
C. AD = 3 6
D. AD = 6 3



